已知圆 $C:x^2+y^2=2$，直线 $l:x+2y-4=0$，点 $P\left(x_0,y_0\right)$ 在直线 $l$ 上．若存在圆 $C$ 上的点 $Q$，使得 $\angle OPQ=45^\circ$（$O$ 为坐标原点），则 $x_0$ 的取值范围是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
B
【解析】
首先寻找对圆的视角等于 $90^\circ$ 的点的轨迹，显然这是一个封闭曲线为圆 $x^2+y^2=4$．那么在该圆内部的点对圆 $C$ 的视角均大于 $90^\circ$，必然存在使 $\angle OPQ=45^\circ$ 的点；同时在圆外部的点对圆的视角均小于 $90^\circ$，一定不可能使得 $\angle OPQ=45^\circ$．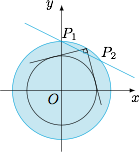
由此分析不难得出，所求点 $P$ 的取值集合为直线 $l:x+2y-4=0$ 被圆 $x^2+y^2=4$ 所截得的线段 $P_1P_2$．设 $P\left(x_0,\dfrac 12\left(4-x_0\right)\right)$，则$$x_0^2+\frac 14\left(4-x_0\right)^2\leqslant 4,$$解得$$0\leqslant x_{0}\leqslant \dfrac 85.$$因此 $x_0$ 的取值范围是 $\left[0,\dfrac 85\right]$．
由此分析不难得出，所求点 $P$ 的取值集合为直线 $l:x+2y-4=0$ 被圆 $x^2+y^2=4$ 所截得的线段 $P_1P_2$．设 $P\left(x_0,\dfrac 12\left(4-x_0\right)\right)$，则$$x_0^2+\frac 14\left(4-x_0\right)^2\leqslant 4,$$解得$$0\leqslant x_{0}\leqslant \dfrac 85.$$因此 $x_0$ 的取值范围是 $\left[0,\dfrac 85\right]$．
题目
答案
解析
备注
