已知 $a$ 为常数，$f(x)=x\left(\ln x-ax\right)$ 有两个极值点 $x_1,x_2$（$x_1<x_2$），则 \((\qquad)\)
【难度】
【出处】
2013年高考湖北卷（理）
【标注】
【答案】
D
【解析】
首先计算 $f'(x)=\ln x-2ax+1$，设导函数的零点为 $x=t$，则$$\ln t=2at-1,$$我们熟知函数 $y=\ln x$ 在 $(1,0)$ 处的切线为 $y=x-1$，于是可知 $0<2a<1$ 且 $0<x_1<1<x_2$，如图．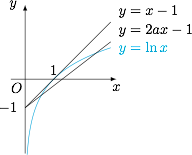
为了消去参数 $a$，将 $a=\dfrac{\ln t+1}{2t}$ 代入函数解析式中可得极值为 $\dfrac 12t\ln t-\dfrac 12t$，记该函数为 $\varphi(t)$，注意到其导函数$$\varphi'(t)=\dfrac 12\ln t,$$于是其图象如图．
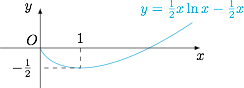由此不难得到 $-\dfrac 12<f(x_1)<0$ 且 $-\dfrac 12<f(x_2)$，选D．
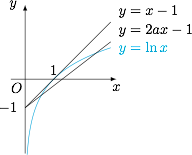为了消去参数 $a$，将 $a=\dfrac{\ln t+1}{2t}$ 代入函数解析式中可得极值为 $\dfrac 12t\ln t-\dfrac 12t$，记该函数为 $\varphi(t)$，注意到其导函数$$\varphi'(t)=\dfrac 12\ln t,$$于是其图象如图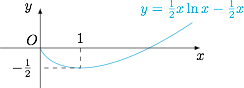．由此不难得到 $-\dfrac 12<f(x_1)<0$ 且 $-\dfrac 12<f(x_2)$，选D．
题目
答案
解析
备注
