已知点 $A$ 在曲线 $P:y=x^2(x>0)$ 上，圆 $A$ 过原点 $O$，且与 $y$ 轴的另一个交点为 $M$．若线段 $OM$，圆 $A$ 和曲线 $P$ 上分别存在点 $B$、点 $C$ 和点 $D$，使得四边形 $ABCD$（点 $A,B,C,D$ 顺时针排列）是正方形，则称点 $A$ 为曲线 $P$ 的"完美点"．那么下列结论中正确的是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
B
【解析】
需要给这道题目配图．当然，除非先计算出了 $A,B,C,D$ 点的准确位置，否则无法准确的画出这个正方形来．因此我们可以在曲线 $P$ 上挑一个 $A$ 的位置，然后在此基础上进行作图尝试．虽然 $A$ 的位置基本是错误的，但如果我们使用尽量保证图形靠近正方形的作图法，就可以通过调整 $A$ 点的位置，将图形调整为正方形．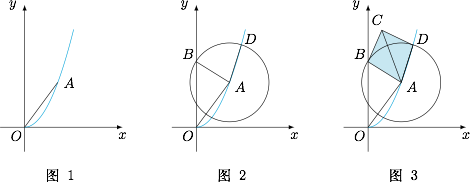
如图 $1$，连接 $OA$，则 $OA$ 的长度就是正方形的对角线长；
如图 $2$，以 $A$ 为圆心，$\dfrac{OA}{\sqrt 2}$ 为半径作圆，取该圆与 $y$ 轴交点中上方的一个为 $B$，取该圆与抛物线交点中上方的一个为 $D$（这是因为点 $A,B,C,D$ 顺时针排列）；
如图 $3$，作 $\angle BAD$ 的平分线，并截取 $AC=AO$；
调整 $A$ 的位置，使得 $\angle BAD=90^\circ$ 即可．
接下来，考虑这样的位置能否找到；如果能找到，有几个？设 $A$ 的坐标为 $A(m,m^2)$．则 $m$ 至少为 $1$，否则无法找到 $B$．当 $m=1$ 时，显然 $\angle BAD$ 为钝角；而当 $m$ 逐渐增大时，将 $\angle BAD$ 分割为两个部分 $\alpha$ 与 $\beta$，如图 $4$．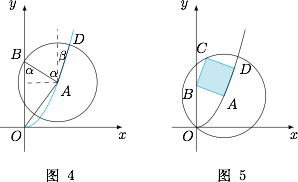
很明显，这两个部分都单调递减，且趋于 $0$（想一想，为什么？）于是满足条件的 $A$ 的位置必然存在，且唯一，选B．最后附上插画师的完成效果图，如图 $5$．
如图 $1$，连接 $OA$，则 $OA$ 的长度就是正方形的对角线长；如图 $2$，以 $A$ 为圆心，$\dfrac{OA}{\sqrt 2}$ 为半径作圆，取该圆与 $y$ 轴交点中上方的一个为 $B$，取该圆与抛物线交点中上方的一个为 $D$（这是因为点 $A,B,C,D$ 顺时针排列）；
如图 $3$，作 $\angle BAD$ 的平分线，并截取 $AC=AO$；
调整 $A$ 的位置，使得 $\angle BAD=90^\circ$ 即可．
接下来，考虑这样的位置能否找到；如果能找到，有几个？设 $A$ 的坐标为 $A(m,m^2)$．则 $m$ 至少为 $1$，否则无法找到 $B$．当 $m=1$ 时，显然 $\angle BAD$ 为钝角；而当 $m$ 逐渐增大时，将 $\angle BAD$ 分割为两个部分 $\alpha$ 与 $\beta$，如图 $4$．
很明显，这两个部分都单调递减，且趋于 $0$（想一想，为什么？）于是满足条件的 $A$ 的位置必然存在，且唯一，选B．最后附上插画师的完成效果图，如图 $5$．
题目
答案
解析
备注
