如图，已知 $\triangle ABC$ 的面积为 $2$，$D,E$ 分别为边 $AB,AC$ 上的点，$F$ 为线段 $DE$ 上一点，设 $\dfrac{AD}{AB}=x,\dfrac{AE}{AC}=y,\dfrac{DF}{DE}=z,$ 且 $y+z-x=1$，则 $\triangle BDF$ 面积的最大值为 \((\qquad)\) 
【难度】
【出处】
2011年清华大学等七校联考自主招生试题
【标注】
【答案】
D
【解析】
如图，连接 $BE$，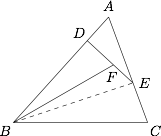
结合 $\dfrac{AD}{AB}=x,\dfrac{AE}{AC}=y,\dfrac{DF}{DE}=z,$，则\[\begin{split} S_{\triangle BDF}&=z\cdot S_{\triangle BDE}=\left( {1 - x} \right)z\cdot S_{\triangle BAE} = \left( {1 - x} \right)yz\cdot S_{\triangle ABC}\\&= 2\left( {1 - x} \right)yz\leqslant 2{\left( {\frac{{1 - x + y + z}}{3}} \right)^3} = \dfrac{{16}}{{27}}.\end{split}\]因此，$\triangle BDF$ 的面积的最大值为 $\dfrac{16}{27}$．
结合 $\dfrac{AD}{AB}=x,\dfrac{AE}{AC}=y,\dfrac{DF}{DE}=z,$，则\[\begin{split} S_{\triangle BDF}&=z\cdot S_{\triangle BDE}=\left( {1 - x} \right)z\cdot S_{\triangle BAE} = \left( {1 - x} \right)yz\cdot S_{\triangle ABC}\\&= 2\left( {1 - x} \right)yz\leqslant 2{\left( {\frac{{1 - x + y + z}}{3}} \right)^3} = \dfrac{{16}}{{27}}.\end{split}\]因此，$\triangle BDF$ 的面积的最大值为 $\dfrac{16}{27}$．
题目
答案
解析
备注
