查看数据源：59b62304b04965000728300f
已知两个半径不等的圆盘叠放在一起（有一轴穿过它们的圆心），两圆盘上分别有互相垂直的两条直径将其分为四个区域，小圆盘上所写的实数分别记为 $x_1,x_2,x_3,x_4$，大圆盘上所写的实数分别记为 $y_1,y_2,y_3,y_4$，如图所示．将小圆盘逆时针旋转 $i (i=1,2,3,4)$ 次，每次转动 $90^\circ$，记 $T_i (i=1,2,3,4)$ 为转动 $i$ 次后各区域内两数乘积之和，例如 $T_1=x_1y_2+x_2y_3+x_3y_4+x_4y_1$．若\[x_1+x_2+x_3+x_4<0, y_1+y_2+y_3+y_4<0\]则以下结论正确的是 \((\qquad)\)
A: $T_1,T_2,T_3,T_4$ 中至少有一个为正数
B: $T_1,T_2,T_3,T_4$ 中至少有一个为负数
C: $T_1,T_2,T_3,T_4$ 中至多有一个为正数
D: $T_1,T_2,T_3,T_4$ 中至多有一个为负数
【难度】
【出处】
无
【标注】
  • 题型
    >
    组合数学
    >
    组合证明
  • 方法
    >
    论述方式
    >
    反证法
【答案】
A
【解析】
因为\[T_1+T_2+T_3+T_4=\left(x_1+x_2+x_3+x_4\right)\left(y_1+y_2+y_3+y_4\right)>0,\]所以 $T_1,T_2,T_3,T_4$ 中至少有一个为正数．下面分别给出 $T_1,T_2,T_3,T_4$ 中有 $1,2,3,4$ 个正数的例子．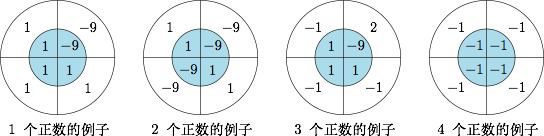
题目 答案 解析 备注
0.181880s