查看数据源：599165bf2bfec200011dfbc4
设复数 $z=\left(x-1\right)+y\mathrm i\left(x,y\in \mathbb R\right)$，若 $ \left|z \right|\leqslant 1$，则 $y\geqslant x$ 的概率为 \((\qquad)\)
A: $\dfrac 34+\dfrac {1}{2{\mathrm \pi} }$
B: $\dfrac 12+\dfrac {1}{\mathrm \pi} $
C: $\dfrac 12-\dfrac {1}{\mathrm \pi} $
D: $\dfrac 14-\dfrac {1}{2{\mathrm \pi} }$
【难度】
【出处】
无
【标注】
【答案】
D
【解析】
根据 $\left|z\right|$ 的几何意义，并结合已知条件可知，点 $(x,y)$ 的轨迹是一个圆及其内部，然后画出直线 $y=x$ 上方的部分，用几何概型知识解决即可．提示：满足题意条件的复数 $ z $ 在复平面上所对应的点是以 $\left(1,0\right) $ 为圆心，$ 1 $ 为半径的圆及其内部的点，其中满足 $y\geqslant x$ 的是图中阴影部分．则 $y\geqslant x$ 的概率就是阴影部分的面积和圆的面积比．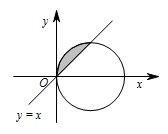
题目 答案 解析 备注
0.110626s