查看数据源：599165c02bfec200011dff1e
某几何体三视图如图所示，则该几何体的体积为 \((\qquad)\)
A: $8 - 2{\mathrm \pi} $
B: $8 - {\mathrm \pi} $
C: $8 - \dfrac{\mathrm \pi} {2}$
D: $8 - \dfrac{\mathrm \pi} {4}$
【难度】
【出处】
无
【标注】
【答案】
B
【解析】
由三视图知该几何体为组合体，而且是一个正方体挖去了部分旋转体．该几何体为一个正方体切掉两个四分之一圆柱剩余的部分，如图所示，所以其体积为\[2\times 2\times 2-2\times \left(\dfrac 14 \times{\mathrm \pi} \times 1^2 \right)\times 2=8-{\mathrm \pi} .\]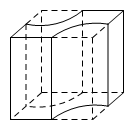
题目 答案 解析 备注
0.154958s