设 $\overrightarrow a$ 是已知的平面向量且 $\overrightarrow a \ne\overrightarrow 0$．关于向量 $\overrightarrow a$ 的分解，有如下四个命题：
① 给定向量 $\overrightarrow b$，总存在向量 $\overrightarrow c$，使 $\overrightarrow a = \overrightarrow b + \overrightarrow c$；
② 给定向量 $\overrightarrow b$ 和 $\overrightarrow c$，总存在实数 $\lambda $ 和 $\mu $，使 $\overrightarrow a = \lambda \overrightarrow b + \mu \overrightarrow c$；
③ 给定单位向量 $\overrightarrow b$ 和正数 $\mu $，总存在单位向量 $\overrightarrow c$ 和实数 $\lambda $，使 $\overrightarrow a = \lambda \overrightarrow b + \mu \overrightarrow c$；
④ 给定正数 $\lambda $ 和 $\mu $，总存在单位向量 $\overrightarrow b$ 和单位向量 $\overrightarrow c$，使 $\overrightarrow a = \lambda \overrightarrow b + \mu \overrightarrow c$．
上述命题中的向量 $\overrightarrow b,\overrightarrow c$ 和 $\overrightarrow a$ 在同一平面内且两两不共线，则真命题的个数是 \((\qquad)\)
① 给定向量 $\overrightarrow b$，总存在向量 $\overrightarrow c$，使 $\overrightarrow a = \overrightarrow b + \overrightarrow c$；
② 给定向量 $\overrightarrow b$ 和 $\overrightarrow c$，总存在实数 $\lambda $ 和 $\mu $，使 $\overrightarrow a = \lambda \overrightarrow b + \mu \overrightarrow c$；
③ 给定单位向量 $\overrightarrow b$ 和正数 $\mu $，总存在单位向量 $\overrightarrow c$ 和实数 $\lambda $，使 $\overrightarrow a = \lambda \overrightarrow b + \mu \overrightarrow c$；
④ 给定正数 $\lambda $ 和 $\mu $，总存在单位向量 $\overrightarrow b$ 和单位向量 $\overrightarrow c$，使 $\overrightarrow a = \lambda \overrightarrow b + \mu \overrightarrow c$．
上述命题中的向量 $\overrightarrow b,\overrightarrow c$ 和 $\overrightarrow a$ 在同一平面内且两两不共线，则真命题的个数是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
B
【解析】
本小题主要考查了平面向量基本定理以及向量加减法综合应用，命题 ①② 相对较容易判断，命题，命题 ③，$\overrightarrow b$ 给定，即 $\lambda\overrightarrow b$ 所在的直线确定，$\mu\overrightarrow c$ 模长固定，然后结合图形，即可解决；命题 ④，只需意识到向量 $\lambda\overrightarrow b$ 与 $\mu\overrightarrow a$ 的模长固定，即可判断命题 ④．利用平面向量基本定理进行判断．
①，取 $\overrightarrow{c}=\overrightarrow{a}-\overrightarrow{b}$，知 ① 正确；
②，因为 $\overrightarrow b$ 和 $\overrightarrow c$ 不共线，由平面向量基本定理知，② 正确；
对于 ③④：
作 $\overrightarrow{OA}=\overrightarrow{a}$，$\overrightarrow{OB}=\overrightarrow{b}$，$\overrightarrow{CA}=\overrightarrow{c}$，
当 $\overrightarrow{b}$ 确定时，若 $\overrightarrow{OB'}=\lambda \overrightarrow{b}$，则 $B'$ 在直线 $OB$ 上运动；当 $\lambda$ 确定时，$B'$ 在以 $O$ 为圆心，$|\lambda|$ 为半径的圆上运动；当 $\mu$ 确定时，若 $\overrightarrow{C'A}=\mu \overrightarrow{c}$，则 $C'$ 在以 $A$ 为圆心，$|\mu|$ 为半径的圆上运动．
当 $B'$ 与 $C'$ 重合时，有 $\overrightarrow{a}=\lambda \overrightarrow{b}+\mu\overrightarrow{c}$．
对于 ③，当直线 $OB$ 与以 $A$ 为圆心，$\mu$ 为半径的圆无公共点时，$B'$ 与 $C'$ 不可能重合，此时不存在单位向量 $\overrightarrow c$ 和实数 $\lambda $ 满足条件；
如图：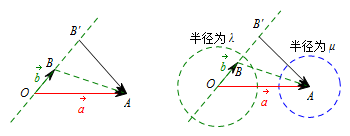
对于 ④，如果以 $O$ 为圆心 $\lambda$ 为半径的圆，与以 $A$ 为圆心，$\mu$ 为半径的圆无公共点，不存在满足条件的向量，故 ④ 错误．
①，取 $\overrightarrow{c}=\overrightarrow{a}-\overrightarrow{b}$，知 ① 正确；
②，因为 $\overrightarrow b$ 和 $\overrightarrow c$ 不共线，由平面向量基本定理知，② 正确；
对于 ③④：
作 $\overrightarrow{OA}=\overrightarrow{a}$，$\overrightarrow{OB}=\overrightarrow{b}$，$\overrightarrow{CA}=\overrightarrow{c}$，
当 $\overrightarrow{b}$ 确定时，若 $\overrightarrow{OB'}=\lambda \overrightarrow{b}$，则 $B'$ 在直线 $OB$ 上运动；当 $\lambda$ 确定时，$B'$ 在以 $O$ 为圆心，$|\lambda|$ 为半径的圆上运动；当 $\mu$ 确定时，若 $\overrightarrow{C'A}=\mu \overrightarrow{c}$，则 $C'$ 在以 $A$ 为圆心，$|\mu|$ 为半径的圆上运动．
当 $B'$ 与 $C'$ 重合时，有 $\overrightarrow{a}=\lambda \overrightarrow{b}+\mu\overrightarrow{c}$．
对于 ③，当直线 $OB$ 与以 $A$ 为圆心，$\mu$ 为半径的圆无公共点时，$B'$ 与 $C'$ 不可能重合，此时不存在单位向量 $\overrightarrow c$ 和实数 $\lambda $ 满足条件；
如图：
对于 ④，如果以 $O$ 为圆心 $\lambda$ 为半径的圆，与以 $A$ 为圆心，$\mu$ 为半径的圆无公共点，不存在满足条件的向量，故 ④ 错误．
题目
答案
解析
备注
