本题考查立体几何的反射问题，既可按照反射的定义，在正方体内部研究直线的反射，也可以把正方体进行平移、拓展成一个更大的棱柱，只研究直线所经过的平面．法一：
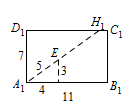
先作出过三点 $A,A_1,E$ 的截面 $AA_1H_1H$，如图：由题意知，第一、二次反射线都在平面 $AA_1H_1H$ 上，先在矩形 $A_1B_1C_1D_1$ 中计算出 $H_1$ 点的位置，
知 $A_1E=5$，从而有 $\tan\angle EA_1B_1=\dfrac 34=\dfrac{A_1D_1}{D_1H_1}$，故 $D_1H_1=\dfrac{28}{3}<11$，故 $A_1H_1=\dfrac{35}{3}$，$H_1$ 在边 $C_1D_1$ 上．
在矩形 $AHH_1A_1$ 中分析 $L_1,L_2,L_3$，如图，$L_1=AE=EF=L_2=13$，$L_3=FG$．
由 $\dfrac{GH}{FH}=\dfrac{12}{5}=\dfrac{GH}{\frac{35}{3}-10}$ 得 $GH=4$，从而 $L_3=\dfrac{13}{3}$．
我们来分析最后一张反射线，即光线 $FG$ 被平面 $CDD_1C_1$ 反射后的光线位置．
首先，我们作出 $GG'\perp 平面CDD_1C_1$，交平面 $ABB_1A_1$ 于点 $G'$．
反射光线一定在由 $FGG'$ 构成的平面内，作出该截面，为矩形 $MM'L'L$，如图：在各个截面内进行计算，要比较 $L_3$ 与 $L_4$ 的大小，只需比较 $GL$ 与 $MG$ 的大小，
也只需比较 $LH$ 与 $CH$ 的大小，而 $LH=\dfrac 43$，$CH=\dfrac 53$，从而 $L_3<L_4$．
法二：
光线发出的方向向量为 $\left(4,3,12\right)$，不妨设光线速度不变，为 $13$，则线段长度比等于时间比．
在不考虑反射的情况下，则经过时间 $t_1$，光线到达点的坐标为 $\left(4t_1,3t_1,12t_1\right)$．又点 $C_1$ 的坐标为 $\left(11,7,13\right)$，故当某个坐标分量达到 $0$ 或 $C_1$ 点坐标对应的分量时，光线会进行反射．
当 $t_1=1$ 时，有 $12t_1=12$，此时光线到达长方体的上平面，坐标为 $\left(4,3,12\right)$，并进行反射；
再经过时间 $t_2$ 时，光线到达点的坐标为 $\left(4+4t_2,3+3t_2,12-12t_2\right)$，当 $t_2=1$ 时，光线到达下底面，坐标为 $\left(8,6,0\right)$；
再经过 $t_3$ 时，光线到达点的坐标为 $\left(8+4t_3,6+3t_3,12t_3\right)$．于是 $t_3=\dfrac 13$ 时，光线到达后平面，坐标为 $\left(\dfrac{28}{3},7,4\right)$；
同理，$\dfrac{28}{3}+4t_4=11$，即 $t_4=\dfrac{5}{12}$ 时，光线遇到右平面．
由 $t_3<t_4=t_1=t_2$ 知，$L_3<L_4<L_1=L_2$．
以上过程可以通过下面的示意图理解：