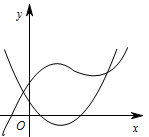
在同一直角坐标系中,函数 $y = a{x^2} - x + \dfrac{a}{2}$ 与 $y = {a^2}{x^3} - 2a{x^2} + x + a\left(a \in {\mathbb {R}}\right)$ 的图象不可能的是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
B
【解析】
本题考查利用导数研究函数单调性的问题.两个函数解析式比较复杂,其图象的特点关键在于单调性、极值的研究,需要借助导数工具进行.当 $a = 0 $ 时,D符合;
当 $a \ne 0$ 时,函数 $y = a{x^2} - x + \dfrac{a}{2}$ 的图象的对称轴为直线 $ x = \dfrac 1 {2a} $,对函数 $y = {a^2}{x^3} - 2a{x^2} + x + a$ 求导得\[y' = 3{a^2}{x^2} - 4ax +1= \left(3ax-1\right)\left(ax-1\right),\]令 $y'=0 $,则\[ {x_1} = \dfrac 1 {3a} , {x_2}= \dfrac 1 a ,\]所以对称轴 $x=\dfrac 1 {2a} $ 介于两个极值点 ${x_1} = \dfrac 1 {3a} $,$ {x_2}= \dfrac 1 a $ 之间,所以B是错误的.
当 $a \ne 0$ 时,函数 $y = a{x^2} - x + \dfrac{a}{2}$ 的图象的对称轴为直线 $ x = \dfrac 1 {2a} $,对函数 $y = {a^2}{x^3} - 2a{x^2} + x + a$ 求导得\[y' = 3{a^2}{x^2} - 4ax +1= \left(3ax-1\right)\left(ax-1\right),\]令 $y'=0 $,则\[ {x_1} = \dfrac 1 {3a} , {x_2}= \dfrac 1 a ,\]所以对称轴 $x=\dfrac 1 {2a} $ 介于两个极值点 ${x_1} = \dfrac 1 {3a} $,$ {x_2}= \dfrac 1 a $ 之间,所以B是错误的.
题目
答案
解析
备注