已知点 $A,B$ 分别为异面直线 $a,b$ 上的点，且直线 $AB$ 与 $a,b$ 均垂直，动点 $P\in a$，$Q\in b$，$PA+QB$ 为定值，则线段 $PQ$ 中点 $M$ 的轨迹是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
A
【解析】
作直线 $a,b$ 以及点 $P,Q$ 在线段 $AB$ 的中垂面上的投影，记为直线 $a',b'$ 以及点 $P',Q'$，则线段 $P'Q'$ 的中点即点 $M$，这样就把空间的问题转化成为了平面上的问题，如图．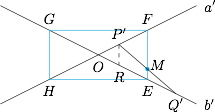
设 $PA+QB=2m$，而 $OE=OF=OG=OH=m$．以 $P',Q'$ 分别在射线 $OF,OE$ 上为例．
由$$OP'+OQ'=AP+BQ=2m,$$以及 $OE+OF=2m$，可得 $FP'=EQ'$．
过 $P'$ 作直线 $EF$ 的平行线交直线 $b'$ 于点 $R$，则有$$FP'=ER=EQ',$$于是线段 $P'Q'$ 的中点 $M$ 在线段 $EF$ 上．
类似的，可得其他情形时点 $M$ 的轨迹分别为线段 $FG$，$GH$，$HE$．
综上所述，线段 $PQ$ 中点 $M$ 的轨迹是矩形 $EFGH$．
设 $PA+QB=2m$，而 $OE=OF=OG=OH=m$．以 $P',Q'$ 分别在射线 $OF,OE$ 上为例．由$$OP'+OQ'=AP+BQ=2m,$$以及 $OE+OF=2m$，可得 $FP'=EQ'$．
过 $P'$ 作直线 $EF$ 的平行线交直线 $b'$ 于点 $R$，则有$$FP'=ER=EQ',$$于是线段 $P'Q'$ 的中点 $M$ 在线段 $EF$ 上．
类似的，可得其他情形时点 $M$ 的轨迹分别为线段 $FG$，$GH$，$HE$．
综上所述，线段 $PQ$ 中点 $M$ 的轨迹是矩形 $EFGH$．
题目
答案
解析
备注
