已知事件“在矩形 $ABCD$ 的边 $CD$ 上随机取一点 $P$，使 $\triangle APB$ 的最大边是 $AB$”发生的概率为 $\dfrac{1}{2}$，则 $\dfrac{AD}{AB} = $ \((\qquad)\)
【难度】
【出处】
2013年高考湖南卷（文）
【标注】
【答案】
D
【解析】
先根据概率 $\dfrac 12$ 这个条件找到使 $AB=EB$ 或 $AB=AE$ 时点 $E$ 在 $CD$ 的位置．然后求出 $\dfrac {AD}{AB}$．由于满足条件的概率为 $\dfrac{1}{2}$，且点 $P$ 在边 $CD$ 上运动，根据图形的对称性，当点 $P$ 在靠近点 $D$ 的 $CD$ 边的 $\dfrac{1}{4}$ 分点时，$EB = AB$（当点 $P$ 超过点 $E$ 向点 $D$ 运动时，$PB > AB$）．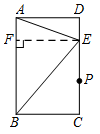
设 $AB = x$，过点 $E$ 作 $EF \perp AB$ 交 $AB$ 于点 $F$，则 $BF = \dfrac{3}{4}x$．
在 $\mathrm{Rt} \triangle FBE$ 中，因为\[E{F^2} = B{E^2} - F{B^2} = A{B^2} - F{B^2} = \dfrac{7}{16}{x^2},\]即 $EF = \dfrac{\sqrt 7 }{4}x$，所以 $\dfrac{AD}{AB} = \dfrac{\sqrt 7 }{4}$．
设 $AB = x$，过点 $E$ 作 $EF \perp AB$ 交 $AB$ 于点 $F$，则 $BF = \dfrac{3}{4}x$．在 $\mathrm{Rt} \triangle FBE$ 中，因为\[E{F^2} = B{E^2} - F{B^2} = A{B^2} - F{B^2} = \dfrac{7}{16}{x^2},\]即 $EF = \dfrac{\sqrt 7 }{4}x$，所以 $\dfrac{AD}{AB} = \dfrac{\sqrt 7 }{4}$．
题目
答案
解析
备注
