已知函数 $y=f(x)$,$x\in\mathbb{R}$ 满足 $f(x+2)=2f(x)$,且 $x\in[-1,1]$ 时,$f(x)=-|x|+1$,则当 $x\in[-10,10]$ 时,$y=f(x)$ 与 $g(x)=\log_4|x|$ 的图像的交点个数为 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
C
【解析】
由题意,函数 $f(x)$ 满足:定义域为 $\rm{R}$,且 $f(x+2)=2f(x)$,当 $x\in [-1,1]$ 时,$f(x)=-|x|+1$,在同一坐标系中画出满足条件的函数 $f(x)$ 与函数 $y=\log_4|x|$ 的图像如图,由图像知这两个函数在区间 $[-10,10]$ 内共有11个交点.因此本题选C.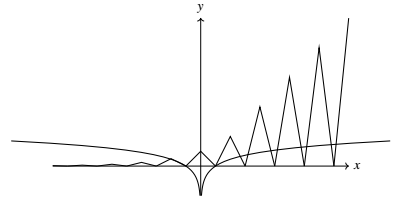

题目
答案
解析
备注