设 $f\left(x\right),g\left(x\right),h\left(x\right)$ 是定义域为 $\mathbb R$ 的三个函数,对于命题:① 若 $f\left(x\right)+g\left(x\right)$,$f\left(x\right)+h\left(x\right)$,$g\left(x\right)+h\left(x\right)$ 均为增函数,则 $f\left(x\right),g\left(x\right),h\left(x\right)$ 中至少有一个增函数;② 若 $f\left(x\right)+g\left(x\right)$,$f\left(x\right)+h\left(x\right)$,$g\left(x\right)+h\left(x\right)$ 均是以 $T$ 为周期的函数,则 $f\left(x\right),g\left(x\right),h\left(x\right)$ 均是以 $T$ 为周期的函数,下列判断正确的是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
D
【解析】
命题 ①,常函数既不是增函数也不是减函数的函数,故可以构造分段函数,举出反例;命题 ②,可以通过解方程,将函数用周期函数表示出.① 为假命题,我们可以如下构造反例.将定义域 $ \mathbb R $ 分为三段,函数 $ f\left(x\right) $ 在第一段上是水平的射线(若要构造严格单调的反例,可以将水平的线段或射线改为斜率为 $ -1 $ 的线段或射线,斜率为 $ 1 $ 的线段或射线改为斜率为 $ 2 $ 的线段或射线.),函数 $ g\left(x\right) $ 在第二段上是水平的线段,函数 $ h\left(x\right) $ 在第三段上是水平的射线,而在其余的部分,三个函数均为斜率为 $ 1 $ 的线段或射线.那么在每一段上,$ f\left(x\right)+g\left(x\right),g\left(x\right)+h\left(x\right),h\left(x\right)+f\left(x\right) $ 均为斜率为 $ 1 $ 或 $ 2 $ 的线段或射线,如图.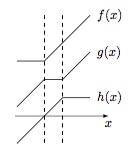 ② 为真命题.令\[\begin{split}F\left(x\right)&=f\left(x\right)+g\left(x\right),\\G\left(x\right)&=f\left(x\right)+h\left(x\right),\\H\left(x\right)&=g\left(x\right)+h\left(x\right),\end{split}\]是以 $ T $ 为周期的函数,同理 $ g\left(x\right),h\left(x\right) $ 也是以 $ T $ 为周期的函数.
② 为真命题.令\[\begin{split}F\left(x\right)&=f\left(x\right)+g\left(x\right),\\G\left(x\right)&=f\left(x\right)+h\left(x\right),\\H\left(x\right)&=g\left(x\right)+h\left(x\right),\end{split}\]是以 $ T $ 为周期的函数,同理 $ g\left(x\right),h\left(x\right) $ 也是以 $ T $ 为周期的函数.
综上所述,选D.
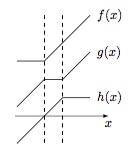 ② 为真命题.令\[\begin{split}F\left(x\right)&=f\left(x\right)+g\left(x\right),\\G\left(x\right)&=f\left(x\right)+h\left(x\right),\\H\left(x\right)&=g\left(x\right)+h\left(x\right),\end{split}\]是以 $ T $ 为周期的函数,同理 $ g\left(x\right),h\left(x\right) $ 也是以 $ T $ 为周期的函数.
② 为真命题.令\[\begin{split}F\left(x\right)&=f\left(x\right)+g\left(x\right),\\G\left(x\right)&=f\left(x\right)+h\left(x\right),\\H\left(x\right)&=g\left(x\right)+h\left(x\right),\end{split}\]是以 $ T $ 为周期的函数,同理 $ g\left(x\right),h\left(x\right) $ 也是以 $ T $ 为周期的函数.综上所述,选D.
题目
答案
解析
备注