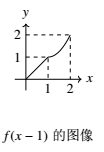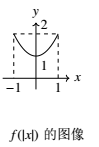已知 $f(x)=\begin{cases}
x+1,\quad x\in[-1,0),\\x^2+1,\quad x\in[0,1],
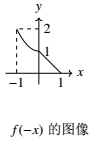
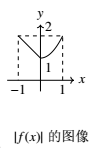
\end{cases}$ 则下列函数的图像错误的是 \((\qquad)\)
x+1,\quad x\in[-1,0),\\x^2+1,\quad x\in[0,1],
\end{cases}$ 则下列函数的图像错误的是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
D
【解析】
依题意,作函数 $f(x)$ 的图像,A.将 $f(x)$ 的图像向右平移一个单位,即得到 $f(x-1)$ 的图像,所以A正确;B.$f(-x)$ 与 $f(x)$ 的图像关于 $y$ 轴对称,所以B正确;C.$f(x)$ 的定义域关于原点对称,$f(|x|)$ 是偶函数,即 $f(|x|)$ 在 $x\in[0, 1]$ 上的图像与 $f(x)$ 在 $x\in[0, 1]$ 上的图像相同,$f(|x|)$ 在 $x\in[-1, 0)$ 上的图像与 $f(x)$ 在 $x\in(0, 1]$ 时的图像相同,所以C正确;D.因为 $f(x)\geqslant 0$,所以 $|f(x)|=f(x)$,即 $|f(x)|$ 的图像与 $f(x)$ 的图像相同,所以D不正确.
题目
答案
解析
备注