已知函数 $f(x)=\begin{cases}2-|x|,&x\leqslant 2,\\ (x-2)^2,&x>2,\end{cases}$ 函数 $g(x)=b-f(2-x)$，其中 $b\in\mathbb R$．若函数 $y=f(x)-g(x)$ 恰有 $4$ 个零点，则 $b$ 的取值范围是 \((\qquad)\)
【难度】
【出处】
2015年高考天津卷（理）
【标注】
【答案】
D
【解析】
函数 $y=f(x)-g(x)$ 的零点，即函数 $h(x)=f(x)+f(2-x)$ 的图象与直线 $y=b$ 的公共点的横坐标．接下来研究函数 $h(x)$．
显然 $h(x)$ 关于直线 $x=1$ 对称（因为 $h(2-x)=h(x)$），因此考察其在区间 $[1,+\infty )$ 上的图象，然后再通过对称变换即可得到函数 $h(x)$ 的图象．
事实上，按 $x$ 与 $1$，$2$ 的大小讨论可得当 $x\geqslant 1$ 时，有$$h(x)=\begin{cases} (2-|x|)+(2-|2-x|),1\leqslant x\leqslant 2,\\ (x-2)^2+2-|2-x|,x>2,\end{cases}$$即$$h(x)=\begin{cases} 2,1\leqslant x\leqslant 2,\\x^2-5x+8,x>2,\end{cases}$$因此函数 $h(x)$ 的图象如图．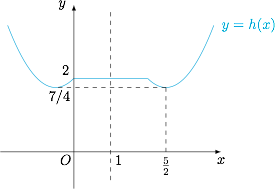
从而若函数 $h(x)$ 的图象与直线 $y=b$ 有 $4$ 个不同的公共点，那么 $b$ 的取值范围是 $\left(\dfrac 74,2\right)$．
显然 $h(x)$ 关于直线 $x=1$ 对称（因为 $h(2-x)=h(x)$），因此考察其在区间 $[1,+\infty )$ 上的图象，然后再通过对称变换即可得到函数 $h(x)$ 的图象．
事实上，按 $x$ 与 $1$，$2$ 的大小讨论可得当 $x\geqslant 1$ 时，有$$h(x)=\begin{cases} (2-|x|)+(2-|2-x|),1\leqslant x\leqslant 2,\\ (x-2)^2+2-|2-x|,x>2,\end{cases}$$即$$h(x)=\begin{cases} 2,1\leqslant x\leqslant 2,\\x^2-5x+8,x>2,\end{cases}$$因此函数 $h(x)$ 的图象如图．
从而若函数 $h(x)$ 的图象与直线 $y=b$ 有 $4$ 个不同的公共点，那么 $b$ 的取值范围是 $\left(\dfrac 74,2\right)$．
题目
答案
解析
备注
