设 $m,k$ 为整数，方程 $mx^2-kx+2=0$ 在区间 $(0,1)$ 内有两个不同的根，则 $m+k$ 的最小值为 \((\qquad)\)
【难度】
【出处】
2011年高考重庆卷（理）
【标注】
【答案】
D
【解析】
容易得到 $m,k$ 均为正整数．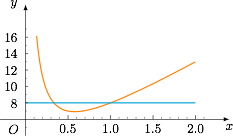
分离变量，有 $k=mx+\dfrac 2x$，于是问题转化为直线 $y=k$ 与对勾函数 $y=mx+\dfrac 2x$ 的图象的两个交点的横坐标均在区间 $(0,1)$ 上，于是$$2\sqrt{2m}<k<m+2,$$注意到 $m+2$ 为整数，于是在区间 $\left(2\sqrt{2m},m+2\right)$ 上存在整数 $k$ 的充要条件为$$m+2-2\sqrt{2m}>1,$$解得$$m>3+2\sqrt 2,$$于是 $m$ 的最小值为 $6$，而 $k$ 的最小值为 $7$．故 $m+k$ 的最小值为 $13$．
分离变量，有 $k=mx+\dfrac 2x$，于是问题转化为直线 $y=k$ 与对勾函数 $y=mx+\dfrac 2x$ 的图象的两个交点的横坐标均在区间 $(0,1)$ 上，于是$$2\sqrt{2m}<k<m+2,$$注意到 $m+2$ 为整数，于是在区间 $\left(2\sqrt{2m},m+2\right)$ 上存在整数 $k$ 的充要条件为$$m+2-2\sqrt{2m}>1,$$解得$$m>3+2\sqrt 2,$$于是 $m$ 的最小值为 $6$，而 $k$ 的最小值为 $7$．故 $m+k$ 的最小值为 $13$．
题目
答案
解析
备注
