设函数 $f_1(x)=x^2$，$f_2(x)=2\left(x-x^2\right)$，$f_3(x)=\dfrac 13\left|\sin 2\pi x\right|$，$a_i=\dfrac{i}{99}$，$i=0,1,2,\cdots,99$．记$$I_k=\left|f_k(a_0)-f_k(a_1)\right|+\left|f_k(a_1)-f_k(a_2)\right|+\cdots+\left|f_k(a_{98})-f_k(a_{99})\right|,k=1,2,3,$$则 \((\qquad)\)
【难度】
【出处】
2014年高考浙江卷（理）
【标注】
【答案】
B
【解析】
如图（为了便于观察，将原题中的 $100$ 个点修改为了 $20$ 个点），所求 $I_k$ 的几何意义就是散点图的相邻点位差和．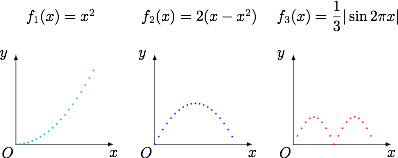
比较散点图和连续的图象可知，如果出现“高峰”或者“低谷”，则可能有位差和的损失．而避免位差和损失的唯一方法就是将“峰顶”或者“谷底”包含在离散点集内．对于左图和中图，无损失时位差和显然为 $1$，因此很容易得到 $I_1=1$，而 $I_2<1$．对于右图，无损失时位差和为 $\dfrac 43$，因此虽然在转化为散点图的时候位差和有所损失，但损失极小，因此 $I_3\approx \dfrac 43$．于是 $I_2<I_1=1<I_3<\dfrac 43$．
比较散点图和连续的图象可知，如果出现“高峰”或者“低谷”，则可能有位差和的损失．而避免位差和损失的唯一方法就是将“峰顶”或者“谷底”包含在离散点集内．对于左图和中图，无损失时位差和显然为 $1$，因此很容易得到 $I_1=1$，而 $I_2<1$．对于右图，无损失时位差和为 $\dfrac 43$，因此虽然在转化为散点图的时候位差和有所损失，但损失极小，因此 $I_3\approx \dfrac 43$．于是 $I_2<I_1=1<I_3<\dfrac 43$．
题目
答案
解析
备注
