设 $x\in{\mathbb{R}}$,$\left[x\right]$ 表示不超过 $x$ 的最大整数,若存在实数 $t$,使得 $\left[t\right]=1$,$\left[t^2\right]=2$,$\cdots$,$\left[t^n\right]=n$ 同时成立,则正整数 $n$ 的最大值是 \((\qquad)\)
【难度】
【出处】
2015年高考湖北卷(理)
【标注】
【答案】
B
【解析】
如图,将 $\left[t^n\right]=n$ 的解$$n^{\frac 1n}\leqslant t<\left(n+1\right)^{\frac 1n}, n=1,2,\cdots$$分别标在数轴上(注意幂的大小比较,如比较 $2^{\frac 12}$ 和 $3^{\frac 13}$ 时可以通过比较 $2^3$ 和 $3^2$ 进行),记这些区间分别为 $A_1,A_2,\cdots$,则有$$\bigcap_{k=1}^4A_k=\left[3^{\frac 13},5^{\frac 14}\right),$$而$$\bigcap_{k=1}^5A_k=\varnothing.$$于是所求正整数 $n$ 的最大值是 $4$.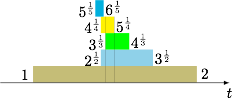

题目
答案
解析
备注