查看数据源：590acd6f6cddca00092f6ff7
函数 $f(x)=ax^3+bx^2+cx+d$ 的图象如图所示，则下列结论成立的是 \((\qquad)\)
A: $a>0,b<0,c>0,d>0$
B: $a>0,b<0,c<0,d>0$
C: $a<0,b<0,c>0,d>0$
D: $a>0,b<0,c>0,d<0$
【难度】
【出处】
2015年高考安徽卷（文）
【标注】
  • 知识点
    >
    微积分初步
    >
    三次函数的图象与性质
【答案】
A
【解析】
如图，根据函数 $f(x)$ 的图象在 $x=0$ 和 $x\to +\infty$ 的取值可以得到 $d>0$，$a>0$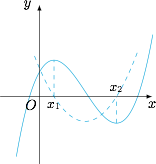；根据导函数 $f'(x)=3ax^2+2bx+c$ 的两根之和和两根之积均大于零可以得到 $b<0$，$c>0$．
综上所述，结论成立的是A．
题目 答案 解析 备注
0.109480s