查看数据源：590a765f6cddca00092f6e3c
已知定义在 $\left[{0,1}\right]$ 上的函数 $f\left( x \right)$ 满足：
① $f\left( 0 \right) = f\left( 1 \right) = 0$；
② 对所有 $x,y \in \left[{0,1}\right]$，且 $x \ne y$，有 $\left|{f\left( x \right) - f\left( y \right)}\right| < \dfrac{1}{2}\left|{x - y}\right|$．
若对所有满足条件的 $f(x)$，均有对任意 $x,y \in \left[{0,1}\right]$，$\left|{f\left( x \right) - f\left( y \right)}\right| < k$ 恒成立，则 $k$ 的最小值为 \((\qquad)\)
A: $\dfrac{1}{2}$
B: $\dfrac{1}{4}$
C: $\dfrac{1}{{2{\mathrm \pi}}}$
D: $\dfrac{1}{8}$
【难度】
【出处】
2014年高考辽宁卷（理）
【标注】
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    绝对值函数
  • 题型
    >
    不等式
    >
    恒成立与存在性问题
  • 方法
    >
    思考方式
    >
    从极端情形出发
【答案】
B
【解析】
题意即函数在区间 $[0,1]$ 端点处的函数值相等（均为 $0$）且函数值的变化率的绝对值小于 $\dfrac 12$，求满足该条件的函数 $f(x)$ 的值域长度的最大值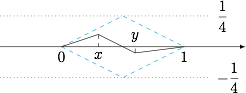．如图，当函数 $f(x)$ 无限接近$$f(x)=\begin{cases} \dfrac 12x,0\leqslant x\leqslant \dfrac 12,\\\dfrac 12(1-x),\dfrac 12<x\leqslant 1\end{cases}$$时，$f(x)$ 的值域长度无限接近 $\dfrac 14$，因此 $k\geqslant \dfrac 14$．
下面证明当 $k=\dfrac 14$ 时符合题意．
若 $x=y$，则显然有 $\forall x,y \in \left[{0,1}\right]$，$\left|{f\left( x \right) - f\left( y \right)}\right| < k$；
若 $x\neq y$，对任意 $x,y\in [0,1]$，不妨设 $x<y$，有\[\begin{split} 2\left|f(x)-f(y)\right|&\leqslant \left|f(x)-f(0)\right|+\left|f(x)-f(y)\right|+\left|f(1)-f(y)\right|\\
&< \dfrac 12x+\dfrac 12(y-x)+\dfrac 12(1-y)\\
&=\dfrac 12,\end{split}\]因此 $\left|f(x)-f(y)\right|< k$，符合题意．
综上，$k$ 的最小值为 $\dfrac 14$．
题目 答案 解析 备注
0.108565s