查看数据源：590bde7d6cddca0008611028
若 $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ 均为单位向量，且 $\overrightarrow{a}\cdot\overrightarrow{b}=0$，$\left(\overrightarrow{a}-\overrightarrow{c}\right)\cdot\left(\overrightarrow{b}-\overrightarrow{c}\right)\leqslant 0$，则 $\left|\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}\right|$ 的最大值为 \((\qquad)\)
A: $\sqrt{2}-1$
B: $1$
C: $\sqrt{2}$
D: $2$
【难度】
【出处】
2011年高考辽宁卷（理）
【标注】
  • 知识点
    >
    解析几何
    >
    圆
    >
    圆的定义
    >
    等张角线
【答案】
B
【解析】
分别用 $\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$ 表示向量 $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$，则有$$OA\perp OB,OA=OB=OC=1,\angle ACB\geqslant 90^\circ.$$如图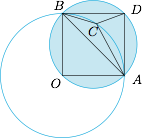．从而有$$\left|\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}\right|=|DC|\in[\sqrt 2-1,1].$$
题目 答案 解析 备注
0.127042s