在平面直角坐标系 $xOy$ 中，已知向量 $\overrightarrow a ,\overrightarrow b$，$\big|\overrightarrow a \big| = \big|\overrightarrow b \big| = 1$，$\overrightarrow a\cdot \overrightarrow b = 0$，点 $Q$ 满足 $\overrightarrow{OQ}= \sqrt 2 \left(\overrightarrow a + \overrightarrow b \right)$．曲线$$C = \left\{ P\left|\right.\overrightarrow{OP}= \overrightarrow a \cos \theta + \overrightarrow b \sin \theta ,0 \leqslant \theta < 2{\mathrm \pi} \right\},$$区域$$ \Omega = \left\{ P\left|\right.0 < r \leqslant{\big|\overrightarrow{PQ}\big|}\leqslant R,r < R\right\}.$$若 $C \cap \Omega$ 为两段分离的曲线，则 \((\qquad)\)
【难度】
【出处】
2014年高考安徽卷（理）
【标注】
【答案】
A
【解析】
整个问题的条件和结论都与相对位置有关，和绝对位置无关，因此可以忽略平面直角坐标系 $xOy$ 这一束缚．
如图，长度均为 $1$ 的有向线段 $\overrightarrow{OA}\perp\overrightarrow{OB}$，分别代表 $\overrightarrow a$ 和 $\overrightarrow b$．易得 $\overrightarrow{OQ}$ 在 $\angle AOB$ 的平分线上，与 $\overrightarrow{OA}$ 和 $\overrightarrow{OB}$ 的夹角均为 $45^\circ$，且 $|OQ|=2$．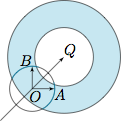
对于曲线 $C$，注意到 $\overrightarrow{OP}$ 在 $\overrightarrow a$ 和 $\overrightarrow b$ 上的有向投影分别为 $\cos\theta$ 和 $\sin\theta$，因此曲线 $C$（即 $P$ 点的轨迹）是以 $O$ 为圆心，$1$ 为半径的圆（且 $\theta$ 为以 $\overrightarrow{OA}$ 为始边，$\overrightarrow{OP}$ 为终边的角），记为圆 $O$．
对于区域 $\Omega$，容易得到它表示以 $Q$ 为圆心，外圆半径为 $R$，内圆半径为 $r$ 的圆环内部（包括内外边界）．
于是 $C\cap\Omega$ 表示圆 $O$ 被 $\Omega$ 表示的圆环所截的部分，为了保证它为两段分离的曲线，需要圆环的内圆和外圆均与圆 $O$ 相交，因此 $1<r<R<3$．
如图，长度均为 $1$ 的有向线段 $\overrightarrow{OA}\perp\overrightarrow{OB}$，分别代表 $\overrightarrow a$ 和 $\overrightarrow b$．易得 $\overrightarrow{OQ}$ 在 $\angle AOB$ 的平分线上，与 $\overrightarrow{OA}$ 和 $\overrightarrow{OB}$ 的夹角均为 $45^\circ$，且 $|OQ|=2$．
对于曲线 $C$，注意到 $\overrightarrow{OP}$ 在 $\overrightarrow a$ 和 $\overrightarrow b$ 上的有向投影分别为 $\cos\theta$ 和 $\sin\theta$，因此曲线 $C$（即 $P$ 点的轨迹）是以 $O$ 为圆心，$1$ 为半径的圆（且 $\theta$ 为以 $\overrightarrow{OA}$ 为始边，$\overrightarrow{OP}$ 为终边的角），记为圆 $O$．对于区域 $\Omega$，容易得到它表示以 $Q$ 为圆心，外圆半径为 $R$，内圆半径为 $r$ 的圆环内部（包括内外边界）．
于是 $C\cap\Omega$ 表示圆 $O$ 被 $\Omega$ 表示的圆环所截的部分，为了保证它为两段分离的曲线，需要圆环的内圆和外圆均与圆 $O$ 相交，因此 $1<r<R<3$．
题目
答案
解析
备注
