已知 $x,y$ 满足约束条件 $\begin{cases} x+y-2\leqslant 0,\\x-2y-2 \leqslant 0,\\2x-y+2 \geqslant 0,\end{cases}$ 若 $z=y-ax$ 取得最大值的最优解不唯一，则实数 $a$ 的值为 \((\qquad)\)
【难度】
【出处】
2014年高考安徽卷（理）
【标注】
【答案】
D
【解析】
我们一般将目标函数 $z=y-ax$ 化为直线 $y=ax+z$，从而将 $z$ 看作直线的截距来解决问题．实际上，在学习了向量数量积的坐标运算后，我们还可以利用向量给出更简明的解决方案．
将目标函数 $z=y-ax$，看作向量 $(x,y)$ 与向量 $(-a,1)$ 的数量积．由于向量 $(-a,1)$ 的模为定值，于是数量积的大小取决于可行域内的点在向量 $(-a,1)$ 上的有向投影的大小．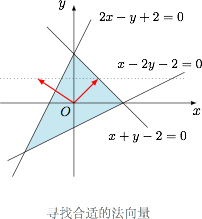
在本题中，目标函数取得最大值的最优解不唯一，这就意味着向量 $(-a,1)$ 与可行域的某个边界垂直，且该边界上的点的有向投影是最大的．不难确定，符合条件的边界为直线 $x+y-2=0$ 和 $2x-y+2=0$，于是它们的纵坐标为 $1$ 的法向量分别为 $(1,1)$ 以及 $(-2,1)$．
将目标函数 $z=y-ax$，看作向量 $(x,y)$ 与向量 $(-a,1)$ 的数量积．由于向量 $(-a,1)$ 的模为定值，于是数量积的大小取决于可行域内的点在向量 $(-a,1)$ 上的有向投影的大小．
在本题中，目标函数取得最大值的最优解不唯一，这就意味着向量 $(-a,1)$ 与可行域的某个边界垂直，且该边界上的点的有向投影是最大的．不难确定，符合条件的边界为直线 $x+y-2=0$ 和 $2x-y+2=0$，于是它们的纵坐标为 $1$ 的法向量分别为 $(1,1)$ 以及 $(-2,1)$．
题目
答案
解析
备注
