查看数据源：59cc68321d3b2000088b6d7c
已知 $\triangle ABC$ 中，$\overrightarrow{CP}=\dfrac 12\left(\overrightarrow{CA}+\overrightarrow{CB}\right)$，$\left|\overrightarrow{CP}\right|=\dfrac 12\left|\overrightarrow{AB}\right|=1$．点 $Q$ 是线段 $AB$ 上一点，且 $\overrightarrow{CQ}\cdot\overrightarrow{CP}=\dfrac 12$，则 $\left|\overrightarrow{CQ}\right|$ 的取值范围是 \((\qquad)\) ．
A: $\left(\dfrac 12,1\right]$
B: $\left(\dfrac 12,+\infty\right)$
C: $\left[\dfrac 12,1\right]$
D: $\left(0,1\right]$
【难度】
【出处】
无
【标注】
  • 知识点
    >
    向量
    >
    向量的运算
    >
    向量的数量积
【答案】
A
【解析】
根据已知条件，$CP$ 为 $\triangle ABC$ 的边 $AB$ 上的中线，且其长度为 $AB$ 的一半．因此 $\triangle ABC$ 为直角三角形，且 $C$ 为直角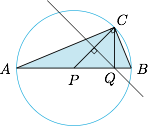．接下来考虑 $\overrightarrow{CQ}\cdot\overrightarrow{CP}=\dfrac 12$，注意到 $CP$ 的长度为定值 $1$，因此这个表达式的几何意义为点 $Q$ 在线段 $CP$ 的垂直平分线上．于是问题转化为 $C$ 点在以线段 $AB$ 为直径的圆（除去 $A,B$ 两点）上运动，求线段 $PC$ 的垂直平分线与线段 $AB$ 的交点 $Q$ 与 $P$ 的距离的取值范围，不难得到答案为 $\left(\dfrac 12,1\right]$．
题目 答案 解析 备注
0.132490s