已知函数 $f(x)=ax^2+bx+c$，且 $a>b>c$，$a+b+c=0$，集合 $A=\{m\mid f(m)<0\}$，则 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
A
【解析】
由题目条件可以得到的信息是$$a>0,c<0,f(1)=0.$$于是我们知道 $f(0)<0$，二次函数 $f(x)$ 的开口向上，一个零点是 $1$，另一个零点 $x_0<1$．
结合选项知，问题集中在 $f(x)$ 的两个零点间的距离与 $3$ 的大小关系，即 $x_{0}$ 与 $-2$ 的大小关系，因为$$f(-2)=4a-2b+c=3(a-b)>0,$$所以 $f(x)$ 的两个零点间距离小于 $3$，如图：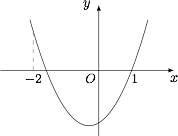
于是知选项 A 正确，形象一点地说，函数 $f(x)$ 在 $x$ 轴下方的部分对应的区间长度小于 $3$，像一条宽度小于 $3$ 的河，从这条河中的任意一点出发，跨出长度为 $3$ 的一步，必然跨过该条河流，对应到 $x$ 轴上方的点．
结合选项知，问题集中在 $f(x)$ 的两个零点间的距离与 $3$ 的大小关系，即 $x_{0}$ 与 $-2$ 的大小关系，因为$$f(-2)=4a-2b+c=3(a-b)>0,$$所以 $f(x)$ 的两个零点间距离小于 $3$，如图：
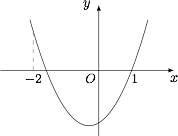于是知选项 A 正确，形象一点地说，函数 $f(x)$ 在 $x$ 轴下方的部分对应的区间长度小于 $3$，像一条宽度小于 $3$ 的河，从这条河中的任意一点出发，跨出长度为 $3$ 的一步，必然跨过该条河流，对应到 $x$ 轴上方的点．
题目
答案
解析
备注
