若 $0<x,y<\dfrac {\pi}{2}$,且 $\sin x=x\cos y$,则 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
C
【解析】
由题意知$$\dfrac {\sin x}{x}=\cos y=t,$$我们可以分别作出两个函数 $t=\dfrac {\sin x}{x}$ 与 $t=\cos x$ 的草图:
因为 $t=\dfrac {\sin x}{x}$ 在 $\left(0,\dfrac {\pi}{2}\right )$ 上单调递减,且 $\dfrac {\sin{x}}{x}>\cos x$(想一想这两个结论如何证明?),所以可以作出它们的草图如下: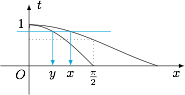 我们得到$$\cos y=\dfrac {\sin x}{x}>\cos x,$$从而有$$y<x.$$下面比较 $y$ 与 $\dfrac x2$ 的大小:
我们得到$$\cos y=\dfrac {\sin x}{x}>\cos x,$$从而有$$y<x.$$下面比较 $y$ 与 $\dfrac x2$ 的大小:
受前面的启发,我们只需要比较它们的余弦值的大小即可,也就是比较 $\dfrac {\sin x}{x}$ 与 $\cos\dfrac x2$ 的大小关系.
考虑边界情况,当 $x=\dfrac{\pi}{2}$ 时,有$$\dfrac{\sin x}{x}=\dfrac {2}{\pi}<\dfrac {\sqrt 2}{2}=\cos\dfrac{\pi}{4},$$有$$y>\dfrac {\pi}{4}=\dfrac x2.$$下面直接给出证明,因为$$ \dfrac {\sin x}{x}=\dfrac {2\sin\dfrac x2\cos\dfrac x2}{x}=\dfrac {\sin\dfrac x2}{\dfrac x2}\cdot \cos\dfrac x2<\cos\dfrac x2,$$从而有 $y>\dfrac x2$.综上有$$\dfrac x2<y<x.$$事实上,函数 $t=\cos x$,$t=\dfrac {\sin x}{x}$ 与 $t=\cos\dfrac{x}{2}$ 有如下关系$$\forall x\in \left(0,\dfrac {\pi}{2}\right ),\cos x<\dfrac {\sin x}{x}<\cos\dfrac x2,$$它们的图象如下: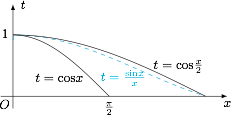
因为 $t=\dfrac {\sin x}{x}$ 在 $\left(0,\dfrac {\pi}{2}\right )$ 上单调递减,且 $\dfrac {\sin{x}}{x}>\cos x$(想一想这两个结论如何证明?),所以可以作出它们的草图如下:
 我们得到$$\cos y=\dfrac {\sin x}{x}>\cos x,$$从而有$$y<x.$$下面比较 $y$ 与 $\dfrac x2$ 的大小:
我们得到$$\cos y=\dfrac {\sin x}{x}>\cos x,$$从而有$$y<x.$$下面比较 $y$ 与 $\dfrac x2$ 的大小:受前面的启发,我们只需要比较它们的余弦值的大小即可,也就是比较 $\dfrac {\sin x}{x}$ 与 $\cos\dfrac x2$ 的大小关系.
考虑边界情况,当 $x=\dfrac{\pi}{2}$ 时,有$$\dfrac{\sin x}{x}=\dfrac {2}{\pi}<\dfrac {\sqrt 2}{2}=\cos\dfrac{\pi}{4},$$有$$y>\dfrac {\pi}{4}=\dfrac x2.$$下面直接给出证明,因为$$ \dfrac {\sin x}{x}=\dfrac {2\sin\dfrac x2\cos\dfrac x2}{x}=\dfrac {\sin\dfrac x2}{\dfrac x2}\cdot \cos\dfrac x2<\cos\dfrac x2,$$从而有 $y>\dfrac x2$.综上有$$\dfrac x2<y<x.$$事实上,函数 $t=\cos x$,$t=\dfrac {\sin x}{x}$ 与 $t=\cos\dfrac{x}{2}$ 有如下关系$$\forall x\in \left(0,\dfrac {\pi}{2}\right ),\cos x<\dfrac {\sin x}{x}<\cos\dfrac x2,$$它们的图象如下:

题目
答案
解析
备注