已知椭圆 $\dfrac{x^2}{16}+\dfrac{y^2}{4}=1$ 的左右焦点分别为 $F_1,F_2$，点 $P$ 在直线 $l:x-\sqrt 3y+8+2\sqrt 3=0$ 上，当 $\angle F_1PF_2$ 取最大值时，$\dfrac{PF_1}{PF_2}=$ \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
A
【解析】
和物理中的电场线、磁场线类似，我们可以作出对线段 $F_1F_2$ 的"等张角线"，如图所示：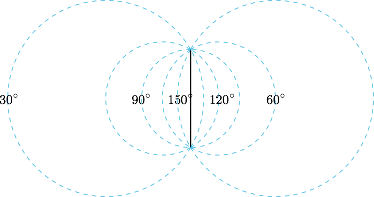
由此可知，取 $F_1F_2$ 的“等张角线”中与直线 $l$ 相切的一条圆弧，则切点位置就是 $\angle F_1PF_2$ 取最大值的位置．从而，设该圆弧的圆心为 $M(0,m)$，则$$\sqrt{12+m^2}=\dfrac{\left|\sqrt 3m-8-2\sqrt 3\right|}{\sqrt{1^2+\left(\sqrt 3\right)^2}},$$解得 $m=2$，或 $m=-2\left(7+8\sqrt 3\right)$．舍去负根，可得 $m=2$，进而圆弧的半径 $R=4$，可计算得 $P\left(-2,2+2\sqrt 3\right)$．因此可计算得$$\dfrac{PF_1}{PF_2}=\sqrt 3-1.$$
由此可知，取 $F_1F_2$ 的“等张角线”中与直线 $l$ 相切的一条圆弧，则切点位置就是 $\angle F_1PF_2$ 取最大值的位置．从而，设该圆弧的圆心为 $M(0,m)$，则$$\sqrt{12+m^2}=\dfrac{\left|\sqrt 3m-8-2\sqrt 3\right|}{\sqrt{1^2+\left(\sqrt 3\right)^2}},$$解得 $m=2$，或 $m=-2\left(7+8\sqrt 3\right)$．舍去负根，可得 $m=2$，进而圆弧的半径 $R=4$，可计算得 $P\left(-2,2+2\sqrt 3\right)$．因此可计算得$$\dfrac{PF_1}{PF_2}=\sqrt 3-1.$$
题目
答案
解析
备注
