查看数据源：59cc9b14310996000af46a82
如图，在平面直角坐标系 $xOy$ 中，$A(-1,0)$，$B(1,0)$．点 $C$ 是单位圆上一点，且其纵坐标大于 $0$，延长 $AC$ 到 $P$，使 $CP=CB$．当点 $C$ 从 $B$ 点运动到 $A$ 点时，点 $P$ 运动的轨迹长度为 \((\qquad)\) ．
A: $\pi$
B: $2\pi$
C: $3\pi$
D: 以上答案都不对
【难度】
【出处】
无
【标注】
  • 题型
    >
    解析几何
    >
    轨迹问题
  • 知识点
    >
    解析几何
    >
    圆
    >
    圆的定义
    >
    等张角线
【答案】
D
【解析】
根据题意，点 $P$ 是点 $B$ 关于 $\angle BCP$ 的平分线 $l$ 对称的点，而 $l$ 是 $\angle ACB$ 的外角平分线．注意到 $\angle ACB$ 的角平分线恒过点 $E(0,-1)$（弧 $AE$ 与弧 $BE$ 相等），而内外角平分线互相垂直，因此 $l$ 与 $CE$ 垂直，进而直线 $l$ 恒过点 $D(0,1)$，如图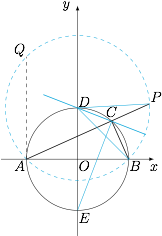．这就意味着 $DP=DB$，因此 $P$ 点在以 $D$ 为圆心，$DB$ 为半径的圆上．考虑到 $C$ 点从 $B$ 点运动到 $A$ 点，因此 $P$ 点从 $B(1,0)$ 点运动到 $Q(-1,2)$ 点，其轨迹长度为\[\dfrac 12\cdot 2\pi \cdot \sqrt 2=\sqrt 2\pi.\]
题目 答案 解析 备注
0.199597s