查看数据源：59113467e020e70007fbea0a
设集合 $A=\left\{x\big||x-a|<1,x\in\mathbb{R}\right\}$，$B=\left\{x\big||x-b|>2,x\in\mathbb{R}\right\}$，若 $A\subseteq B$，则实数 $a,b$ 必满足 \((\qquad)\)
A: $|a+b|\leqslant 3$
B: $|a+b|\geqslant 3$
C: $|a-b|\leqslant 3$
D: $|a-b|\geqslant 3$
【难度】
【出处】
2010年高考天津卷（理）
【标注】
  • 知识点
    >
    不等式
    >
    解不等式
    >
    解含有绝对值的不等式
  • 知识点
    >
    函数
    >
    集合与映射
    >
    集合与集合的关系
【答案】
D
【解析】
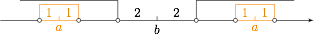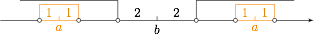常规解法是直接写出集合 $A,B$，再通过它们的关系得到 $a,b$ 满足的式子．但事实上，绝对值是有明确的几何意义的，即数轴上两点之间的距离，所以 $A$ 是由离 $a$ 距离小于 $1$ 的点构成的集合，$B$ 是由离 $b$ 的距离超过 $2$ 的点构成的集合，于是固定 $b$，考虑 $a$ 的范围，如下图：当 $a,b$ 之间的距离不小于 $3$ 时，有 $A\subseteq B$，故D正确．很多与绝对值相关的问题借助距离的几何意义去思考更容易把握住本质．
题目 答案 解析 备注
0.111821s