已知 $a_1,a_2,\cdots ,a_{10}$ 与 $b_1,b_2,\cdots ,b_{10}$ 为互不相同的 $20$ 个实数，若方程$$|x-a_1|+|x-a_2|+\cdots +|x-a_{10}|=|x-b_1|+|x-b_2|+\cdots+|x-b_{10}|$$有有限多个解，则此方程最多有 \((\qquad)\) 个解．
【难度】
【出处】
无
【标注】
【答案】
A
【解析】
问题即函数$$f(x)=|x-a_1|+|x-a_2|+\cdots +|x-a_{10}|-|x-b_1|-|x-b_2|-\cdots -|x-b_{10}|$$的零点个数问题．
我们熟知绝对值函数 $f(x)$ 的图象是一条两条射线与若干条线段连接而成的折线（可以参考每日一题[203]黎明前的黑暗）．在这个问题里，每次折线转折时斜率改变量均为 $2$ 或 $-2$，且每种改变量都取 $10$ 次．
一方面，为了使得函数 $f(x)$ 的零点个数尽可能的多，应当使得斜率改变量依次为$$2,-2,-2,2,2,-2,-2,2,\cdots ,$$如图（示意图中两种改变量分别为 $4$ 次）．并且在实际的构造中，还需要使得折线中每一条非水平的线段穿过 $x$ 轴后再发生转折．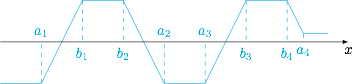
另一方面，由于当 $x$ 很小以及很大时函数 $f(x)$ 的函数值分别为$$a_1+a_2+\cdots +a_{10}-b_1-b_2-\cdots -b_{10}$$以及$$-\left(a_1+a_2+\cdots+a_{10}-b_1-b_2-\cdots -b_{10}\right),$$因此函数 $f(x)$ 的图象中首尾射线均为水平方向，且分居 $x$ 轴的两侧．这样就意味着至少有一条非水平的折线段无法穿过 $x$ 轴．
综合以上两方面可知，此方程最多有 $9$ 个解．
我们熟知绝对值函数 $f(x)$ 的图象是一条两条射线与若干条线段连接而成的折线（可以参考每日一题[203]黎明前的黑暗）．在这个问题里，每次折线转折时斜率改变量均为 $2$ 或 $-2$，且每种改变量都取 $10$ 次．
一方面，为了使得函数 $f(x)$ 的零点个数尽可能的多，应当使得斜率改变量依次为$$2,-2,-2,2,2,-2,-2,2,\cdots ,$$如图（示意图中两种改变量分别为 $4$ 次）．并且在实际的构造中，还需要使得折线中每一条非水平的线段穿过 $x$ 轴后再发生转折．
另一方面，由于当 $x$ 很小以及很大时函数 $f(x)$ 的函数值分别为$$a_1+a_2+\cdots +a_{10}-b_1-b_2-\cdots -b_{10}$$以及$$-\left(a_1+a_2+\cdots+a_{10}-b_1-b_2-\cdots -b_{10}\right),$$因此函数 $f(x)$ 的图象中首尾射线均为水平方向，且分居 $x$ 轴的两侧．这样就意味着至少有一条非水平的折线段无法穿过 $x$ 轴．综合以上两方面可知，此方程最多有 $9$ 个解．
题目
答案
解析
备注
