定义区间 $\left(a,b\right)$,$\left[a,b\right)$,$\left(a,b\right]$,$\left[a,b\right]$ 的长度均为 $d = b - a$,多个区间并集的长度为各区间长度之和,例如,$\left(1,2\right) \cup \left[3,5\right)$ 的长度 $d = \left(2 - 1\right) + \left(5 - 3\right) = 3$.用 $\left[x\right]$ 表示不超过 $x$ 的最大整数,记 $\left\{ x\right\} = x - \left[x\right]$,其中 $x \in {\mathrm {\mathbb{R}}}$.设 $f\left(x\right) = \left[x\right] \cdot \left\{ x\right\} $,$g\left(x\right) = x - 1$,若用 ${d_1}$,$ {d_2} $,${d_3}$ 分别表示不等式 $f\left(x\right) > g\left(x\right)$,方程 $f\left(x\right) = g\left(x\right)$,不等式 $f\left(x\right) < g\left(x\right)$ 解集区间的长度,则当 $0 \leqslant x \leqslant 2011$ 时,有 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
B
【解析】
如图,研究直线 $y=x-1$ 与函数 $y=[x](x-[x])$ 图象的位置关系即可.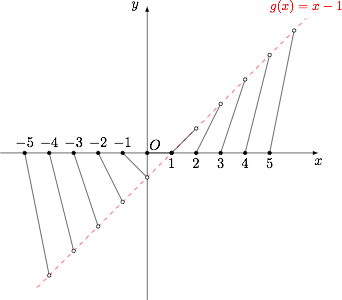

题目
答案
解析
备注