解题的关键在于如何理解条件“$\left| {f\left( {x_1} \right) - f\left( {x_2} \right)} \right| \leqslant 4\left| {{x_1} - {x_2}} \right|$”．
考虑到若 $x_1\neq x_2$，则 $\dfrac {\left|f(x_1)-f(x_2)\right|}{|x_1-x_2|}$ 为割线 $AB$ 斜率的绝对值，其中 $A(x_1,f(x_1))$，$B(x_2,f(x_2))$．
因此在集合 $M$ 中的函数满足的性质为在 $[-1,1]$ 的部分上的任意一条割线斜率绝对值均不超过 $4$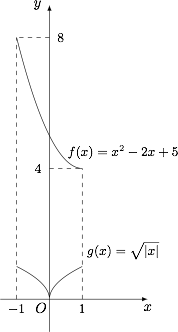．但将条件几何化到这里仍然不足以解决问题，关键在于割线取决于两个动点．
利用极限思想．先固定 $x_1$，当 $x_2$ 无限接近 $x_1$ 时，割线斜率就无限接近于 $f'(x_1)$．这就意味着
$p$：“$x \in [-1,1]$ 时，$|f'{(x+)}|\leqslant 4 $ 且 $|f'{(x-)}|\leqslant 4$”是“$f(x) \in M $”的必要条件．
对于 ${f_1}\left( x \right) = {x^2} - 2x + 5$，${f_1}'(x)=2x-2$，满足条件 $p$；
对于 ${f_2}\left( x \right) = \sqrt {\left| x \right|}$，当 $x>0$ 时，${f_2}'(x)=(\sqrt x)'=\dfrac {1}{2\sqrt{x}}$，不满足条件 $p$．
因此 ${f_2} '(x)\not \in M$，排除A、C；
再由 ${f_1}\left( x \right) = {x^2} - 2x + 5$ 的图象特点，其任意一条割线 $ABb$ 的斜率 $k_{AB}$ 均在 $f'(x_1)$ 和 $f'(x_2)$ 之间，这就意味着在区间 $ (x_1,x_2)$ 上必然存在一点 $x_0$，使得 $f'(x_0)=k_{AB}$．从而由 $|f'{x}|\leqslant 4$ 可得 $|k_{AB}|\leqslant 4$．
因此 ${f_1}(x) \in M $，选D．