查看数据源：59db162334a80e0009f47ca9
若函数 $f\left(x\right)$ 满足条件：当 ${x_1},{ }{x_2} \in \left[ - 1,1\right]$ 时，有 $|f\left({x_1}\right) - f\left({x_2}\right)| \leqslant 3|{x_1} - {x_2}|$ 成立，则称 $f\left(x\right)$ 是“近零稳定函数”．则下列说法中正确的有  \((\qquad)\)
A: $y=x^3$ 是“近零稳定函数”
B: $y=\dfrac{1}{x + 2}$ 是“近零稳定函数”
C: $ y=x\mathrm{e}^x $ 是“近零稳定函数”
D: 以上说法都不对
【难度】
【出处】
无
【标注】
  • 知识点
    >
    微积分初步
    >
    微积分补充知识
    >
    拉格朗日中值定理
  • 知识点
    >
    微积分初步
    >
    利用导数研究函数的性质
    >
    利用导数研究函数的单调性
【答案】
AB
【解析】
如图．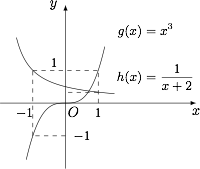
题目 答案 解析 备注
0.170356s