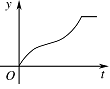
如图,$ |OA|=2 $(单位:$ {\mathrm{m}} $),$ |OB|=1 $(单位:${\mathrm{ m }}$),$ OA $ 与 $ OB $ 的夹角为 $ {\dfrac{\mathrm \pi }{6}} $,以 $ A $ 为圆心,$ AB $ 为半径作圆弧 $ BDC $ 与线段 $ OA $ 的延长线交于点 $ C $.甲、乙两质点同时从点 $ O $ 出发,甲先以速率 $ 1 $(单位:$ {\mathrm{m{/} s }}$)沿线段 $ OB $ 行至点 $ B $,再以速率 $ 3 $(单位:$ {\mathrm{m{/}s}} $)沿圆弧 $ BDC $ 行至点 $ C $ 后停止;乙以速率 $ 2 $(单位:$ {\mathrm{m{/}s}} $)沿线段 $ OA $ 行至点 $ A $ 后停止.设 $ t $ 时刻甲、乙所到达的两点连线与它们经过的路径所围成图形的面积为 $ S\left(t\right)\left(S\left(0\right)= 0\right) $,则函数 $ y=S\left(t\right) $ 的图象大致是 \((\qquad)\) 

【难度】
【出处】
2012年高考江西卷(文)
【标注】
【答案】
A
【解析】
当质点从 $ O $ 点开始运动时,两者行 $ 1 $ 秒后,甲行到 $ B $,乙此时行到 $ A $,设经过 $ t\left(0\leqslant t\leqslant 1\right) $ 秒乙按路径 $ OA $ 所走的路程为 $ 2t $,而对应的甲按路径 $ OB $ 所走的路程为 $ t $,对应的三角形的面积为\[ S={\dfrac{1}{2}}t\times 2t\times \sin {\dfrac{\mathrm \pi }{6}}={\dfrac{1}{2}}t^2\left(0\leqslant t\leqslant 1\right), \]一秒钟后,随着甲的运动,所围成的面积增加值是扇形中 $ AB $ 所扫过的面积\[ S={\dfrac{1}{2}}lr={\dfrac{1}{2}}AB\times 3 \left(t-1\right)={\dfrac{3}{2}}{\sqrt{5-2 \sqrt 3}} \left(t-1\right), \]因此从 $ O $ 出发到达 $ C $ 点时面积变化有以下情况:开始是一个开口向上的二次函数形式,接着是一个一次函数形式,最后是一个常量.
题目
答案
解析
备注