已知函数 $f(x)=ax+\ln x-\dfrac {x^2}{x-\ln x}$ 有三个不同的零点 $x_1,x_2,x_3$（其中 $x_1<x_2<x_3$），则$$\left(1-\dfrac{\ln{x_1}}{x_1}\right)^2\left(1-\dfrac{\ln{x_2}}{x_2}\right)\left(1-\dfrac{\ln{x_3}}{x_3}\right)$$的值为 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
D
【解析】
函数的零点即方程 $(ax+\ln x)(x-\ln x)=x^2$ 的解，因为 $x>0$，所以方程可以变形为$$\left(a+\dfrac {\ln x}{x}\right)\left(1-\dfrac{\ln x}{x}\right)=1.$$令 $t=\dfrac{\ln x}{x}$，记函数 $g(x)=\dfrac{\ln x}{x}$，则有\[g'(x)=\dfrac{1-\ln x}{x^2},\]所以 $g(x)$ 在 $(1,\rm{e})$ 上单调递增，在 $(\rm{e},+\infty)$ 上单调递减，$g(x)_{\max}=\dfrac 1{\rm e}$，$g(x)$ 的图象如下：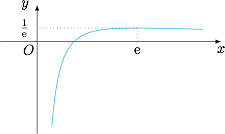
所求方程的解相当于先求一元二次方程 $(a+t)(1-t)=1$ 的解 $t_1,t_2(t_1\leqslant t_2)$，再求方程 $g(x)=t_i,i=1,2$ 的解．
因为方程有三个不同零点，所以 $t_1<t_2\leqslant \dfrac {1}{\rm e}$．
先考虑一元二次方程$$t^2+(a-1)t+1-a=0,$$由判别式 $\Delta >0$ 解得 $a>1$ 或 $a<-3$，由韦达定理知$$t_1+t_2=1-a,t_1t_2=1-a.$$当 $a<-3$ 时，$t_1+t_2=1-a>4$ 与 $t_1<t_2\leqslant \dfrac{1}{\rm e}$ 矛盾，所以$$a>1,t_1<0<t_2<\dfrac 1{\rm e}.$$于是知$$g(x_1)=t_1,g(x_2)=g(x_3)=t_2.$$所求代数式为$$(1-t_1)^2(1-t_2)(1-t_2)=[(1-t_1)(1-t_2)]^2=[1-(t_1+t_2)+t_1t_2]^2=1.$$
所求方程的解相当于先求一元二次方程 $(a+t)(1-t)=1$ 的解 $t_1,t_2(t_1\leqslant t_2)$，再求方程 $g(x)=t_i,i=1,2$ 的解．因为方程有三个不同零点，所以 $t_1<t_2\leqslant \dfrac {1}{\rm e}$．
先考虑一元二次方程$$t^2+(a-1)t+1-a=0,$$由判别式 $\Delta >0$ 解得 $a>1$ 或 $a<-3$，由韦达定理知$$t_1+t_2=1-a,t_1t_2=1-a.$$当 $a<-3$ 时，$t_1+t_2=1-a>4$ 与 $t_1<t_2\leqslant \dfrac{1}{\rm e}$ 矛盾，所以$$a>1,t_1<0<t_2<\dfrac 1{\rm e}.$$于是知$$g(x_1)=t_1,g(x_2)=g(x_3)=t_2.$$所求代数式为$$(1-t_1)^2(1-t_2)(1-t_2)=[(1-t_1)(1-t_2)]^2=[1-(t_1+t_2)+t_1t_2]^2=1.$$
题目
答案
解析
备注
