已知函数 $f(x)=\begin{cases}|\lg(-x)|,&x<0,\\x^2-6x+4,&x>0.\end{cases}$ 若关于 $x$ 的函数 $y=f^2(x)-bf(x)+1$ 有 $8$ 个不同的零点,则实数 $b$ 的取值范围是 \((\qquad)\)
【难度】
【出处】
2015年第二十六届“希望杯”全国数学邀请赛高二(一试)
【标注】
【答案】
C
【解析】
画出 $f(x)$ 的图象如下.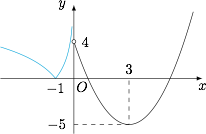 于是直线 $y=t$ 与 $y=f(x)$ 的图象公共点对应关系为\[\begin{array}
于是直线 $y=t$ 与 $y=f(x)$ 的图象公共点对应关系为\[\begin{array}
{c|cccccc} \hline
t&(-\infty,-5)&-5&(-5,0)&0&(0,4)&[4,+\infty)\\ \hline
x&0&1&2&3&4&3 \\ \hline
\end{array}\]因此题意即关于 $t$ 的方程 $t^2-bt+1=0$ 在 $(0,4)$ 上有两个实数解.分离变量,有\[b=t+\dfrac 1t,\]于是实数 $b$ 的取值范围是 $\left(2,\dfrac{17}4\right)$.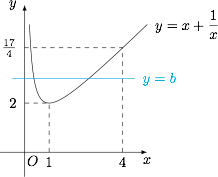
 于是直线 $y=t$ 与 $y=f(x)$ 的图象公共点对应关系为\[\begin{array}
于是直线 $y=t$ 与 $y=f(x)$ 的图象公共点对应关系为\[\begin{array}{c|cccccc} \hline
t&(-\infty,-5)&-5&(-5,0)&0&(0,4)&[4,+\infty)\\ \hline
x&0&1&2&3&4&3 \\ \hline
\end{array}\]因此题意即关于 $t$ 的方程 $t^2-bt+1=0$ 在 $(0,4)$ 上有两个实数解.分离变量,有\[b=t+\dfrac 1t,\]于是实数 $b$ 的取值范围是 $\left(2,\dfrac{17}4\right)$.
题目
答案
解析
备注