查看数据源：59ed8b39c3f07000093ae7d3
已知方程 $3{x^2}-k\cdot\mathrm{e}^x= 0$ 有 $3$ 个实数解，则 $k$ 的值可以是 \((\qquad)\)
A: $\dfrac{3}{\mathrm{e}}$
B: $\dfrac{6}{\mathrm{e}}$
C: $\dfrac{9}{\mathrm{e^2}}$
D: $\dfrac{12}{\mathrm{e^2}}$
【难度】
【出处】
无
【标注】
  • 知识点
    >
    微积分初步
    >
    利用导数研究函数的性质
    >
    利用导数研究函数的零点
  • 知识点
    >
    微积分初步
    >
    导数问题中的技巧
    >
    处理指数的和差化积
【答案】
AC
【解析】
原方程即 $3x^2{\rm e}^{-x}=k$，令 $f(x)=3x^2{\rm e}^{-x}$，则其导函数\[f'(x)=3{\rm e}^{-x}\cdot x(2-x),\]再考虑到\[\lim_{x\to -\infty}f(x)=+\infty,\lim_{x\to +\infty}f(x)=0,\]函数的草图如下，原方程有 $3$ 个实数解．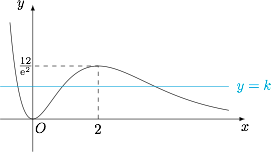
题目 答案 解析 备注
0.114962s