设函数 $f\left(x\right)=\begin{cases}
3x-1,&x<1,\\2^x,&x\geqslant 1,
\end{cases}$ 则满足 $f\left(f\left(a\right)\right)=2^{f\left(a\right)}$ 的 $a$ 的取值范围是 \((\qquad)\)
3x-1,&x<1,\\2^x,&x\geqslant 1,
\end{cases}$ 则满足 $f\left(f\left(a\right)\right)=2^{f\left(a\right)}$ 的 $a$ 的取值范围是 \((\qquad)\)
【难度】
【出处】
2015年高考山东卷(理)
【标注】
【答案】
C
【解析】
由题意可知,$a$ 的取值范围由不等式$$f(a)\geqslant 1$$确定,结合 $f(x)$ 是单调递增函数(如图),可得 $a$ 的取值范围是 $\left[\dfrac 23,+\infty \right)$.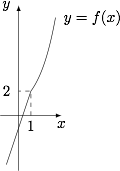

题目
答案
解析
备注