对实数 $a$ 和 $b$，定义运算" $ \otimes $ "：$ a \otimes b = { \begin{cases}
a,&a - b \leqslant 1\\
b,&a - b > 1\\
\end{cases} } $．设函数 $f\left(x\right) = \left({x^2} - 2\right) \otimes \left(x - 1\right),x \in {\mathbb{R}}$．若函数 $y = f\left(x\right) - c$ 的图象与 $x$ 轴恰有两个公共点，则实数 $c$ 的取值范围是 \((\qquad)\)
a,&a - b \leqslant 1\\
b,&a - b > 1\\
\end{cases} } $．设函数 $f\left(x\right) = \left({x^2} - 2\right) \otimes \left(x - 1\right),x \in {\mathbb{R}}$．若函数 $y = f\left(x\right) - c$ 的图象与 $x$ 轴恰有两个公共点，则实数 $c$ 的取值范围是 \((\qquad)\)
【难度】
【出处】
2011年高考天津卷（文）
【标注】
【答案】
B
【解析】
先根据题中对运算的定义将 $f\left(x\right)$ 写成分段函数形式，然后令 $y=f\left(x\right)$ 的图象与直线 $y=c$ 有两个交点即可．函数 $y = f\left(x\right) - c$ 的图象与 $x$ 轴的交点即 $y=f\left(x\right)$ 的图象与直线 $y=c$ 的交点．
依题意可得 $f\left(x\right)= \begin{cases}x^2-2,&-1\leqslant x\leqslant 2,\\ x-1,&x<-1或x>2.\end{cases} $ 其图象如图：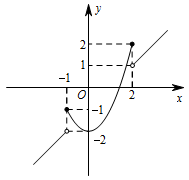
结合图象知，实数 $c $ 应满足范围 $1<c\leqslant 2 $ 或 $ -2<c\leqslant -1 $．
依题意可得 $f\left(x\right)= \begin{cases}x^2-2,&-1\leqslant x\leqslant 2,\\ x-1,&x<-1或x>2.\end{cases} $ 其图象如图：
结合图象知，实数 $c $ 应满足范围 $1<c\leqslant 2 $ 或 $ -2<c\leqslant -1 $．
题目
答案
解析
备注
