若曲线 ${C_1}:{x^2} + {y^2} - 2x = 0$ 与曲线 ${C_2}:y\left(y - mx - m\right) = 0$ 有四个不同的交点,则实数 $m$ 的取值范围是 \((\qquad)\)
【难度】
【出处】
2011年高考江西卷(理)
【标注】
【答案】
B
【解析】
可以根据选项范围的特点,验证特殊值 $m = 0$ 和 $m = 1$,利用排除法解答.观察选项,提炼出待检样例 $m = 0$ 和 $m = 1$.
当 $m = 0$ 时,${C_2}$:${y^2} = 0$ 即 $y = 0$,与 ${C_1}$ 只有两个不同交点,不符合题意,排除A、C;
当 $m = 1$ 时,${C_2}$:$y = 0$ 或 $y = x + 1$,与 ${C_1}$ 交于 $\left( {0 , 0} \right)$、$\left( {2 , 0} \right)$,不符合题意,排除D;选B.
其他解法:
曲线 ${x^2} + {y^2} - 2x = 0$ 表示以 $\left( {1,0} \right)$ 为圆心,以 $ 1 $ 为半径的圆.
曲线 $y\left( {y - mx - m} \right) = 0$ 表示 $y = 0$ 和 $ y - mx - m = 0$ 两条直线.
其中 $ y - mx - m = 0$ 过定点 $\left( { - 1,0} \right)$,而直线 $y = 0$ 与圆有两个交点,故直线 $y - mx - m = 0$ 也应该与圆有两个交点,如图可以知道,临界情况即是直线与圆相切的时候,经计算可得,两种相切情况分别对应\[m = - \frac{\sqrt 3 }{3} 和 m = \frac{\sqrt 3 }{3},\]由图可知,$m$ 的取值范围应为\[\left( { - \frac{\sqrt 3 }{3},0} \right) \cup \left( {0,\frac{\sqrt 3 }{3}} \right).\]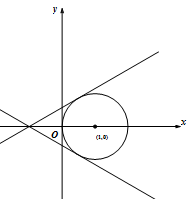
当 $m = 0$ 时,${C_2}$:${y^2} = 0$ 即 $y = 0$,与 ${C_1}$ 只有两个不同交点,不符合题意,排除A、C;
当 $m = 1$ 时,${C_2}$:$y = 0$ 或 $y = x + 1$,与 ${C_1}$ 交于 $\left( {0 , 0} \right)$、$\left( {2 , 0} \right)$,不符合题意,排除D;选B.
其他解法:
曲线 ${x^2} + {y^2} - 2x = 0$ 表示以 $\left( {1,0} \right)$ 为圆心,以 $ 1 $ 为半径的圆.
曲线 $y\left( {y - mx - m} \right) = 0$ 表示 $y = 0$ 和 $ y - mx - m = 0$ 两条直线.
其中 $ y - mx - m = 0$ 过定点 $\left( { - 1,0} \right)$,而直线 $y = 0$ 与圆有两个交点,故直线 $y - mx - m = 0$ 也应该与圆有两个交点,如图可以知道,临界情况即是直线与圆相切的时候,经计算可得,两种相切情况分别对应\[m = - \frac{\sqrt 3 }{3} 和 m = \frac{\sqrt 3 }{3},\]由图可知,$m$ 的取值范围应为\[\left( { - \frac{\sqrt 3 }{3},0} \right) \cup \left( {0,\frac{\sqrt 3 }{3}} \right).\]

题目
答案
解析
备注