设变量 $x,y$ 满足 $\left| x \right| + \left| y \right| \leqslant 1$,则 $x + 2y$ 的最大值和最小值分别为 \((\qquad)\)
【难度】
【出处】
2011年高考安徽卷(理)
【标注】
【答案】
B
【解析】
不等式 $|x| + |y| \leqslant 1$ 对应的平面区域如图所示.当目标函数 $ z=x+2y$ 过点 $\left(0, - 1\right)$,$\left(0,1\right)$ 时,分别取最小值和最大值,所以 $z=x + 2y$ 的最大值和最小值分别为 $ 2、- 2$.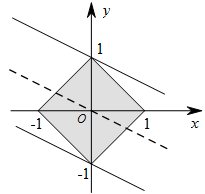

题目
答案
解析
备注