若方程 ${\log_2}(x-3)+2x=4$ 的解是 $x_0$，则不等式 $7x-2x_0\leqslant 1$ 的最大整数解是 \((\qquad)\)
【难度】
【出处】
2010年第二十一届“希望杯”全国数学邀请赛高一（二试）
【标注】
【答案】
C
【解析】
方程\[{\log_2}(x-3)+2x=4\]的解即为函数 $y={\log_2}(x-3)$ 的图象 与直线 $y=4-2x$ 交点的横坐标，如图．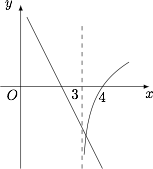
故 $3<x_0<4$．不等式 $7x-2x_0\leqslant 1$ 即为$$x\leqslant \dfrac{2x_0+1}{7},$$而$$1<\dfrac{2x_0+1}{7}<\dfrac 97,$$因此不等式的最大整数解为 $1$．
故 $3<x_0<4$．不等式 $7x-2x_0\leqslant 1$ 即为$$x\leqslant \dfrac{2x_0+1}{7},$$而$$1<\dfrac{2x_0+1}{7}<\dfrac 97,$$因此不等式的最大整数解为 $1$．
题目
答案
解析
备注
