查看数据源：59fad8786ee16400083d2857
已知正方体 $ABCD-A_1B_1C_1D_1$ 的棱长为 $1$，过该正方体的对角线 $BD_1$ 的截面的面积记为 $S$，则 $S$ 的取值范围是 \((\qquad)\)
A: $\left(1,\dfrac{\sqrt 6}{2}\right)$
B: $\left(\dfrac{\sqrt 6}{2},2\right)$
C: $\left(\dfrac{\sqrt 6}{2},\sqrt 2\right)$
D: $\left[\dfrac{\sqrt 6}{2},\sqrt 2\right]$
【难度】
【出处】
2010年第二十一届“希望杯”全国数学邀请赛高一（一试）
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的截面
【答案】
D
【解析】
如图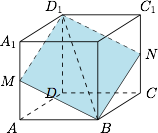．根据正方体的对称性可知，设 $N$ 到直线 $BD_1$ 的距离为 $d$，则\[S=BD_1\cdot d,\]当截面与 $AA_1$ 交点为 $A$ 或 $A_1$ 时，$d$ 最大，此时截面面积最大为 $\sqrt 2$；
当截面与 $AA_1$ 的交点为 $AA_1$ 中点时，$d$ 最小，此时截面面积最小为\[\dfrac 12\cdot \sqrt 3 \cdot \sqrt 2=\dfrac{\sqrt 6}{2}.\]
题目 答案 解析 备注
0.110362s