棱长相等的正四棱锥的相邻侧面所成的二面角的正切值等于 \((\qquad)\)
【难度】
【出处】
2010年第二十一届“希望杯”全国数学邀请赛高二（二试）
【标注】
【答案】
C
【解析】
设正四棱锥 $P-ABCD$ 的棱长为 $2$，取 $PB$ 中点记为 $E$，连接 $AE,CE,AC$，如图．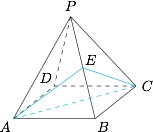
由题可计算，可得$$AE=CE=\sqrt3,AC=2\sqrt2,$$由余弦定理，得$$\cos\angle AEC=\dfrac{AE^2+CE^2-AC^2}{2\cdot AE\cdot CE}=-\dfrac13,$$故所求二面角的正切值等于 $-2\sqrt2$．
由题可计算，可得$$AE=CE=\sqrt3,AC=2\sqrt2,$$由余弦定理，得$$\cos\angle AEC=\dfrac{AE^2+CE^2-AC^2}{2\cdot AE\cdot CE}=-\dfrac13,$$故所求二面角的正切值等于 $-2\sqrt2$．
题目
答案
解析
备注
