已知点 $M$ 在正方体 $ABCD-A_1B_1C_1D_1$ 的棱 $BB_1$ 上,且 $BB_1=3BM$,点 $P$ 在底面 $ABCD$ 内.若 $\angle APA_1=\angle BPM$,则点 $P$ 的轨迹是 \((\qquad)\)
【难度】
【出处】
2010年第二十一届“希望杯”全国数学邀请赛高二(二试)
【标注】
【答案】
A
【解析】
由题可知 $\triangle PAA_1$ 与 $\triangle PBM$ 相似,因此$$\dfrac{PA}{PB}=\dfrac{AA_1}{MB}=3,$$根据阿波罗尼斯圆,点 $P$ 的轨迹是圆的一部分.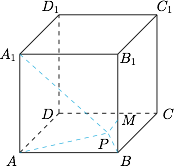

题目
答案
解析
备注