查看数据源：59f85ffd6ee16400083d25ad
若 $x_1$ 是方程 $x{\rm e}^x={\rm e}^2$ 的解，$x_2$ 是方程 $x\ln x={\rm e}^2$ 的解，则 $x_1x_2=$  \((\qquad)\)
A: $1$
B: ${\rm e}$
C: ${\rm e}^2$
D: ${\rm e}^4$
【难度】
【出处】
2017年北京大学优特（U-Test）数学测试试题
【标注】
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的零点
  • 知识点
    >
    函数
    >
    反函数
【答案】
C
【解析】
考虑到 $x_1,x_2$ 分别是函数 $y={\rm e}^x$ 和函数 $y=\ln x$ 与函数 $y=\dfrac{{\rm e}^2}x$ 的公共点 $A,B$ 的横坐标．而 $A,B$ 关于直线 $y=x$ 对称，点 $(x_1,x_2)$ 在反比例函数 $y=\dfrac{{\rm e}^2}x$ 的图象上，因此 $x_1x_2={\rm e}^2$．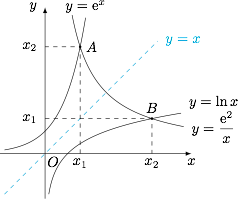
题目 答案 解析 备注
0.109316s