设等比数列 $\left\{ {a_n}\right\} $ 的公比为 $q$，其前 $n$ 项的积为 ${T_n}$，并且满足条件 ${a_1} > 1$，${a_{99}}{a_{100}} - 1 > 0$，$\dfrac{{{a_{99}} - 1}}{{{a_{100}} - 1}} < 0$．给出下列结论：
① $0 < q < 1$；
② ${a_{99}} \cdot {a_{101}} - 1 > 0$；
③ ${T_{100}}$ 的值是 ${T_n}$ 中最大的；
④ 使 ${T_n} > 1$ 成立的最大自然数 $n$ 等于 $ 198 $．
其中正确的结论是 \((\qquad)\)
① $0 < q < 1$；
② ${a_{99}} \cdot {a_{101}} - 1 > 0$；
③ ${T_{100}}$ 的值是 ${T_n}$ 中最大的；
④ 使 ${T_n} > 1$ 成立的最大自然数 $n$ 等于 $ 198 $．
其中正确的结论是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
B
【解析】
由 $\dfrac {a_{99}-1}{a_{100}-1}<0$，可知 $a_{99}$，$a_{100}$ 分居直线 $y=1$ 两侧．而由 $a_{99}a_{100}>0$，可知在 $y=1$ 下方的点必然在 $x$ 轴上方（否则 $a_{99}a_{100}<0$）．从而 $a_{100}<1<a_{99} $（否则与 $a_{1}>1$，且 $\{a_n\}$ 为等比数列矛盾）．因此$$a_1q^{99}<1<a_1^2q^{197},$$如图．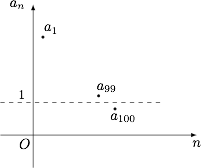
进而可以做出判断：
① 正确，$a_1q^{99}<1<a_1^2q^{197} \Rightarrow 0<q<1$；
② 错误，$a_{99}\cdot a_{101}=a_1^2q^{198}=(a_1q^{99})^2<1$；
③ 错误，$a_{99}>1$，$a_{100}<1 $，于是 $T_{99}$ 最大；
④ 正确，$T_{198}=(a_{99}a_{100})^{99}>1$，$T_{199}=a_{100}^{199}<1$．
进而可以做出判断：① 正确，$a_1q^{99}<1<a_1^2q^{197} \Rightarrow 0<q<1$；
② 错误，$a_{99}\cdot a_{101}=a_1^2q^{198}=(a_1q^{99})^2<1$；
③ 错误，$a_{99}>1$，$a_{100}<1 $，于是 $T_{99}$ 最大；
④ 正确，$T_{198}=(a_{99}a_{100})^{99}>1$，$T_{199}=a_{100}^{199}<1$．
题目
答案
解析
备注
