设不等式组 ${\begin{cases}
x \geqslant a \\
y \geqslant 1 \\
2x + 3y - 35 \leqslant 0 \\
\end{cases}}$ 表示的平面区域是 $W$，则 $W$ 中的整点（即横、纵坐标均为整数的点）共有 $91$ 个，则实数 $a$ 的取值范围是 \((\qquad)\)
x \geqslant a \\
y \geqslant 1 \\
2x + 3y - 35 \leqslant 0 \\
\end{cases}}$ 表示的平面区域是 $W$，则 $W$ 中的整点（即横、纵坐标均为整数的点）共有 $91$ 个，则实数 $a$ 的取值范围是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
C
【解析】
$y=1$ 与 $2x+3y-35=0$ 的交点为 $(16,1)$．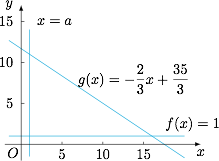
考虑直线 $x=t$（$t\leqslant 16$）在两直线之间部分（包括端点）上的整点个数，从右往左分别为\[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}\hline
t &{16} &{15} &{14} &{13} &{12} &{11} &{10} &9 &8 &\cdots \\ \hline
\text{与}g(x)\text{交点纵坐标}&1&\dfrac 53 &\dfrac 73 &\dfrac 93 &\dfrac{11}{3}&\dfrac{13}{3}&\dfrac{15}{3}&\dfrac{17}{3}&\dfrac {19}{3}&\cdots \\ \hline
\text{整点个数}&1&1&2&3&3&4&5&5&6&\cdots \\ \hline \end{array}\]可以看出整点个数的规律为$$\underbrace{1,1,2}_{4},\underbrace{3,3,4}_{10},\underbrace{5,5,6}_{16},\underbrace{7,7,8}_{22},\underbrace{9,9,10}_{28},11,11,12,\cdots $$因此 $t=1$ 时，整点的总数为 $91$；当 $t=0$ 时，整点总数为 $102$．
因此 $a$ 的取值范围是 $(0,1]$．
考虑直线 $x=t$（$t\leqslant 16$）在两直线之间部分（包括端点）上的整点个数，从右往左分别为\[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}\hlinet &{16} &{15} &{14} &{13} &{12} &{11} &{10} &9 &8 &\cdots \\ \hline
\text{与}g(x)\text{交点纵坐标}&1&\dfrac 53 &\dfrac 73 &\dfrac 93 &\dfrac{11}{3}&\dfrac{13}{3}&\dfrac{15}{3}&\dfrac{17}{3}&\dfrac {19}{3}&\cdots \\ \hline
\text{整点个数}&1&1&2&3&3&4&5&5&6&\cdots \\ \hline \end{array}\]可以看出整点个数的规律为$$\underbrace{1,1,2}_{4},\underbrace{3,3,4}_{10},\underbrace{5,5,6}_{16},\underbrace{7,7,8}_{22},\underbrace{9,9,10}_{28},11,11,12,\cdots $$因此 $t=1$ 时，整点的总数为 $91$；当 $t=0$ 时，整点总数为 $102$．
因此 $a$ 的取值范围是 $(0,1]$．
题目
答案
解析
备注
