查看数据源：592698258044a000098989f1
有四根长都为 $2$ 的直铁条，若再选两根长都为 $a$ 的直铁条，使这六根铁条端点处相连能够焊接成一个三棱锥形的铁架，则 $a$ 的取值范围是 \((\qquad)\)
A: $(0,\sqrt 6+\sqrt 2)$
B: $(1,2\sqrt 2)$
C: $(\sqrt 6-\sqrt 2,\sqrt 6+\sqrt 2)$
D: $(0,2\sqrt 2)$
【难度】
【出处】
2010年高考辽宁卷（理）
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
【答案】
A
【解析】
分两种情况讨论：两根长为 $a$ 的铁条共面和异面．
情形一两根长为 $a$ 的铁条共面
如图，设$$AC=AD=a,BC=CD=DB=AB=2,$$则可得 $a$ 的取值范围为 $(\sqrt 6-\sqrt 2,\sqrt 6 +\sqrt 2)$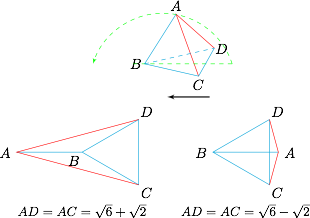．情形二两根长为 $a$ 的铁条异面
如图，设$$AB=CD=a,AC=AD=BC=BD=2,$$则可得 $a$ 的取值范围为 $(0,2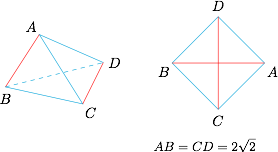\sqrt 2)$．综上，所求 $a$ 的取值范围为 $(0,\sqrt 6+\sqrt 2)$．
题目 答案 解析 备注
0.111619s